Plotting Omics Data

Authors

Jiratchaya Nuanpirom

Prasert Yodsawat

Khunanon Chanasongkram

Published

May 17, 2023

1 Load libraries

pacman::p_load(
  "tidyverse",
  "kableExtra",
  "openxlsx",
  "DESeq2",
  "pcaExplorer",
  "factoextra",
  "ggsci",
  "ComplexHeatmap",
  "RColorBrewer",
  "EnhancedVolcano",
  "ggvenn", 
  "ggpubr",
  "kableExtra"
  )

2 Plotting Abundance of Representative Terms

# Load COG dictionary
COG_dict <- read_delim("https://github.com/JirathNuan/r-handviz-workshop/raw/main/datasets/cog_category.txt")

# Load eggNOG-mapper result
emapper_dt <- read.xlsx("https://github.com/JirathNuan/r-handviz-workshop/raw/main/datasets/Dme_chr4.emapper.annotations.xlsx",
                        startRow = 3, 
                        cols = 7) %>% 
  filter(COG_category != "-") %>%
  group_by(COG_category) %>%
  summarize(n = n()) %>%
  left_join(COG_dict, by = c("COG_category" = "category")) %>%
  mutate(label = paste0(COG_category, ": ", category_name))

# Show first 10 lines of data frame
head(emapper_dt, 10) %>% kbl() %>% kable_styling(full_width = FALSE)
  
# Plot
ggplot(emapper_dt, aes(x = COG_category, y = n, fill = label)) +
  geom_bar(stat = "identity") +
  scale_y_continuous(breaks = seq(0, 100, 10)) +
  labs(x = "COG category",
       y = "Number of sequences", 
       fill = "COG category") +
  theme(legend.key.size = unit(0.5, 'cm'))
1
cog_category.txt is a cluster of orthologous groups (COG) dictionary. Use for look up the category names into the plot.
2
Read eggNOG-mapper result from excel file into emapper_dt, using read.xlsx() from openxlsx library. The excel is read by skipping the first 3 rows and select only 7th column.
3
Then, go to the next step by pipe %>%. This step it to filter unclassified COGs - from the COG_category using dplyr filter().
4
Then group the data frame by COG_category.
5
Count number of COGs presented in this eggNOG-mapper result.
6
Merge COG dictionary into the result using dplyr left_join(). Two data frames are merged by matching the column COG_category from emapper_dt with the column category of COG_dict.
7
Then, add new column label for the plot legend, by append COG category together with the category name.
8
Plot the result from by showing COG_category in x-axis, number of COGs n in y-axis, fill and add legend by column label.
9
Plot bar plot using geom_bar() and stat = "identity"
10
Set y-axis breaks
11
Customize label of x- and y-axis, and legend name in fill.
12
Adjust size of legend using theme(legend.key.size).

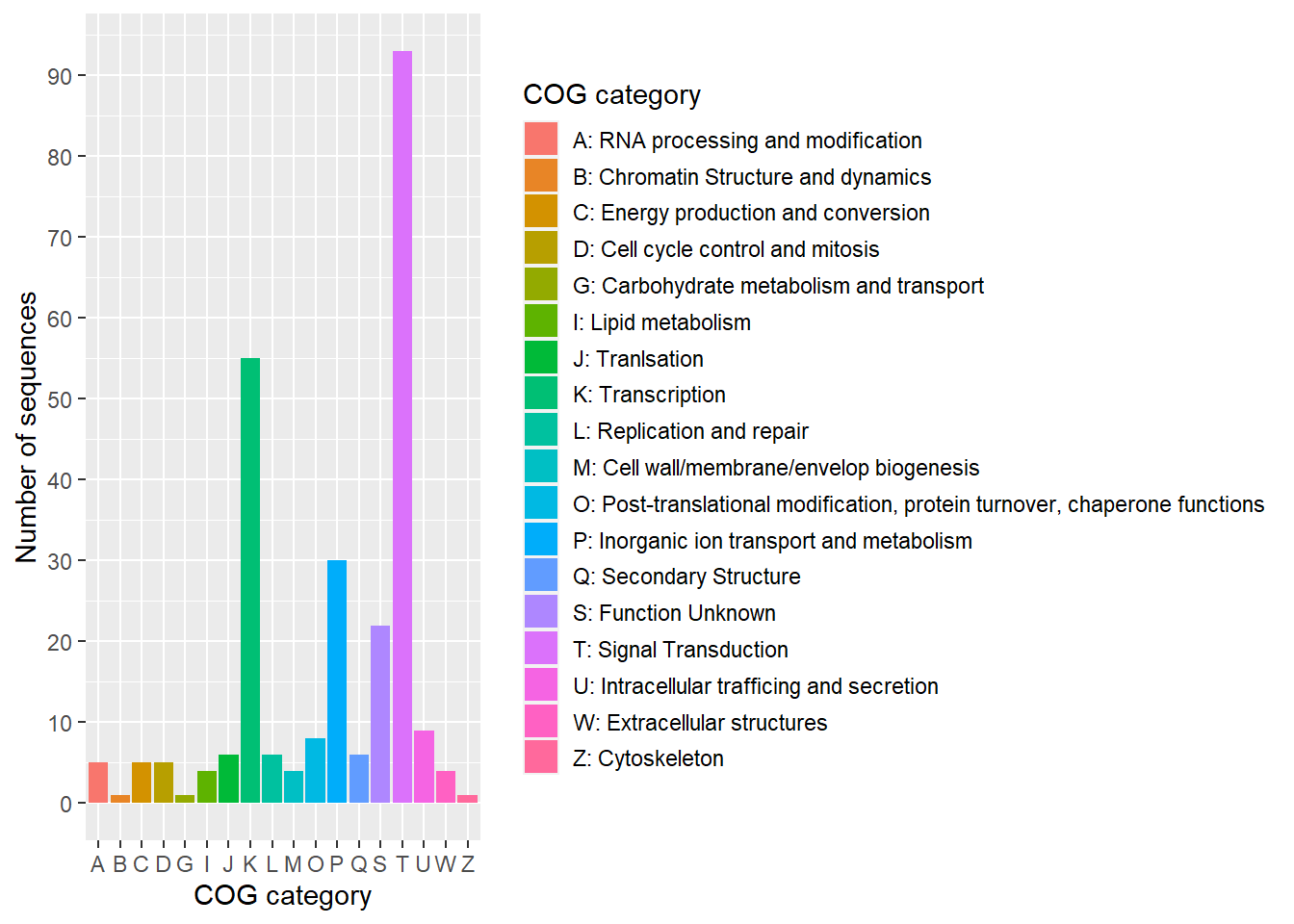
First 10 lines of the number of COG category results.
COG_category n category_name label
A 5 RNA processing and modification A: RNA processing and modification
B 1 Chromatin Structure and dynamics B: Chromatin Structure and dynamics
C 5 Energy production and conversion C: Energy production and conversion
D 5 Cell cycle control and mitosis D: Cell cycle control and mitosis
G 1 Carbohydrate metabolism and transport G: Carbohydrate metabolism and transport
I 4 Lipid metabolism I: Lipid metabolism
J 6 Tranlsation J: Tranlsation
K 55 Transcription K: Transcription
L 6 Replication and repair L: Replication and repair
M 4 Cell wall/membrane/envelop biogenesis M: Cell wall/membrane/envelop biogenesis

3 Principal Component Analysis

Typically, PCA is used for dimensionality reduction to get lower-dimensional data while keeping the most variation possible by taking only the first few principal components. In principle, SVD (singlular value decomposition) or eigenvalues of the data covariance matrix can be used to evaluate the principal components.

From datacamp, The PCA can be more easily computed by following these five steps:

  1. Normalize data: As these data have different scales, performing PCA on them will result in a biased result. In order to ensure that each attribute contributes equally and to prevent one variable from dominating others, the data set needs to be normalized.

  2. Computing the covariable matrix from the normalized data. This is a symmetric matrix, and each element (i, j) corresponds to the covariance between variables i and j.

  3. Get Eigenvectors and eigenvalues: The term eigenvector refers to a direction in mathematics, such as “vertical” or “90 degrees”. By contrast, an eigenvalue represents how much variance there is in a given direction in the data. Therefore, each eigenvector has a corresponding eigenvalue.

  4. Select the principal components: It’s about choosing the eigenvector with the highest eigenvalue that corresponds to the first principal component. The second principal component is the eigenvector with the second highest eigenvalue, etc.

  5. Transforming data into a new form: A new subspace is defined by the principal components, so the original data is re-oriented by multiplying it by the previously computed eigenvectors. As a result of this transformation, the original data doesn’t change, but instead provides a new perspective to better represent it.

We will demonstrate PCA on a pasilla data set (Brooks et al. 2010). This data set was obtained from an experiment on Drosophila melanogaster cell cultures that investigated the effects of knocking down the splicing factor pasilla using RNAi.

# Load data set
cts <- read_delim("https://raw.githubusercontent.com/JirathNuan/r-handviz-workshop/main/datasets/cts.tsv")

# Prepare DESeq input, which is expecting a matrix of integers.
de_input <- as.matrix(cts[,-1])
row.names(de_input)<- cts$transcript_name
# Remove NAs
de_input <- de_input[complete.cases(de_input), ]

# Show first 10 rows of the matrix
kbl(head(de_input, 10))

# Create sample metadata     
coldata <- data.frame(sample = colnames(de_input),
                      sample_group = gsub("[0-9]", "", colnames(de_input)))


# Show how experimental data looks like
kbl(coldata)
1
Load data set into cts data frame, and convert to matrix.
2
Removing NA. The whole row will be deleted if NA is observed.
3
Sample metadata should show a relationship between the sample name (from the matrix column), the sample group, and other experimental design.
treated1 treated2 treated3 untreated1 untreated2 untreated3 untreated4
FBgn0000003 0 0 1 0 0 0 0
FBgn0000008 140 88 70 92 161 76 70
FBgn0000014 4 0 0 5 1 0 0
FBgn0000015 1 0 0 0 2 1 2
FBgn0000017 6205 3072 3334 4664 8714 3564 3150
FBgn0000018 722 299 308 583 761 245 310
FBgn0000022 0 0 0 0 1 0 0
FBgn0000024 10 7 5 10 11 3 3
FBgn0000028 0 1 1 0 1 0 0
FBgn0000032 1698 696 757 1446 1713 615 672
sample sample_group
treated1 treated
treated2 treated
treated3 treated
untreated1 untreated
untreated2 untreated
untreated3 untreated
untreated4 untreated

This workshop will demonstrate data normalization using DESeq2 library.

# Create DESeq object by load matrix and experimental design
dds <- DESeqDataSetFromMatrix(countData = de_input,
                              colData = coldata,
                              design= ~ sample_group)

# Perform differential expression analysis
dds <- DESeq(dds)

# Create a normalized matrix of cts data set
cts_norm <- counts(dds, normalized = TRUE)

# Show how the data looks like
head(cts_norm) %>% kbl()
1
Create DESeq object using count matrix and sample metadata.
2
This function is from DESeq2, to perform differential expression analysis based on the Negative Binomial (a.k.a. Gamma-Poisson) distribution. The analysis started with estimating size factors, estimating dispersion, and fitting the Negative Binomial GLM model and calculate Wald statistics.
3
Create a matrix of normalized count from DESeq2 object after DE analysis.
treated1 treated2 treated3 untreated1 untreated2 untreated3 untreated4
FBgn0000003 0.0000000 0.0000 1.200981 0.000000 0.0000000 0.000000 0.000000
FBgn0000008 85.5968034 115.5963 84.068670 80.824908 89.7936241 117.004615 93.123591
FBgn0000014 2.4456230 0.0000 0.000000 4.392658 0.5577244 0.000000 0.000000
FBgn0000015 0.6114057 0.0000 0.000000 0.000000 1.1154487 1.539534 2.660674
FBgn0000017 3793.7726082 4035.3632 4004.070676 4097.471407 4860.0101913 5486.900612 4190.561607
FBgn0000018 441.4349433 392.7648 369.902150 512.183926 424.4282483 377.185929 412.404476

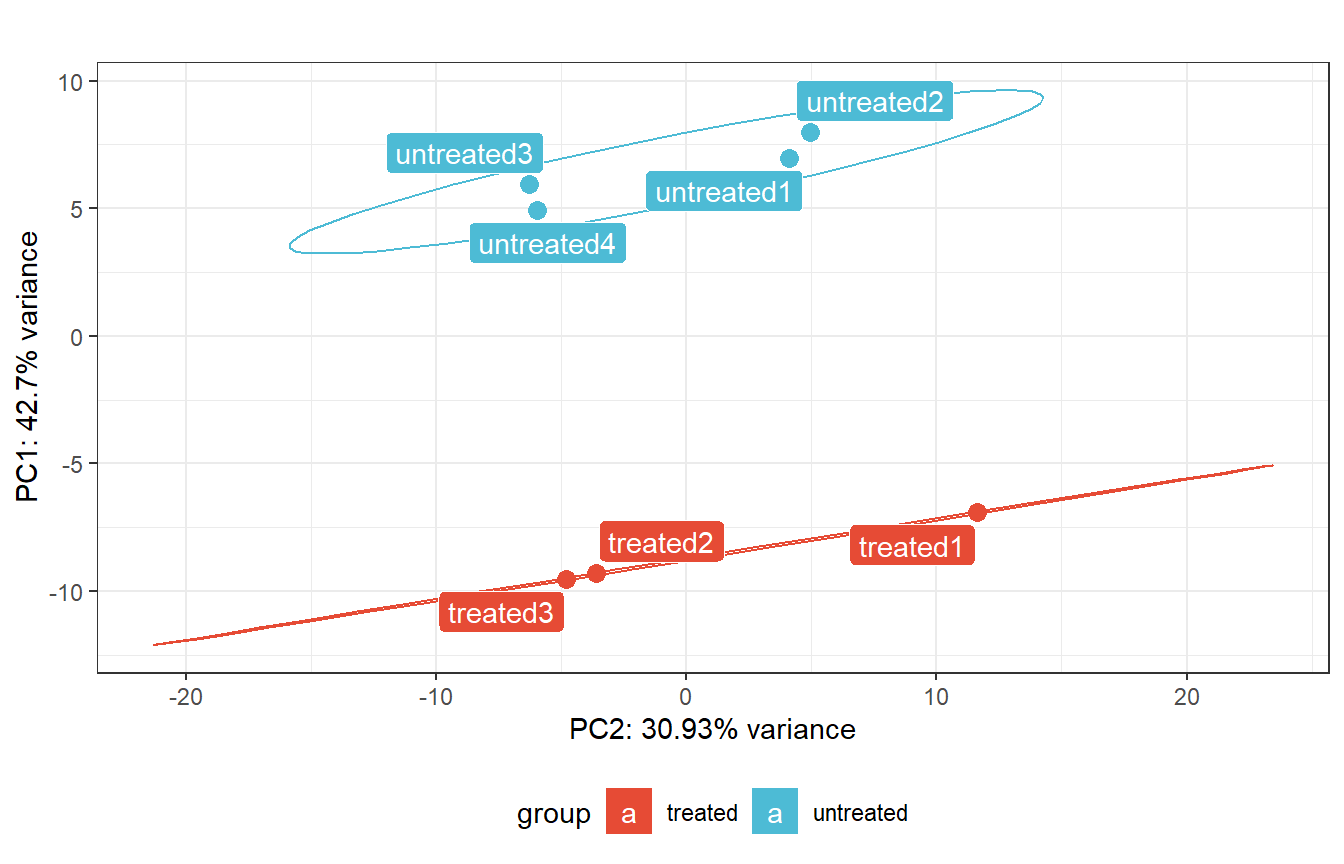
This step is to transform the count matrix through Rlog (regularized log) transforms. Which transform the original count data into log2 scale by fitting a model with a term for each sample and a prior distribution on the coefficients. Use before plotting PCA.

# Plot PCA With pcaExplorer
rld_dds <- rlogTransformation(dds)
pca_dds <- pcaplot(
  rld_dds,
  intgroup = "sample_group",
  ntop = Inf,
  pcX = 1,
  pcY = 2,
  title = "",
  text_labels = TRUE
) +
  scale_fill_npg() +
  scale_color_npg() +
  theme(legend.position = "bottom") +
  coord_flip()
pca_dds
1
Rlog (regularized log) transforms the original count data into log2 scale by fitting a model with a term for each sample and a prior distribution on the coefficients. Use before plotting PCA.
2
Plot PCA

This step is to examine the principal components and visualizing eigenvalues as a scree plot. A scree plot is used to determine the number of significant principal components in a set of data. It is a line graph that shows the eigenvalues of each component in descending order. This helps to identify which components are most important and which can be discarded.

We’ll demonstrate a scree plot using fviz_eig() function from factoextra library.

# Scree plot
pcaobj_dds <- prcomp(t(assay(rld_dds)))

# Visualizing scree plot
fviz_eig(pcaobj_dds, 
         addlabels = TRUE, 
         barfill = pal_npg()(1),
         barcolor = "black",
         title = "Proportion of explained proportion of variance - cts data set",
         ggtheme = theme_gray())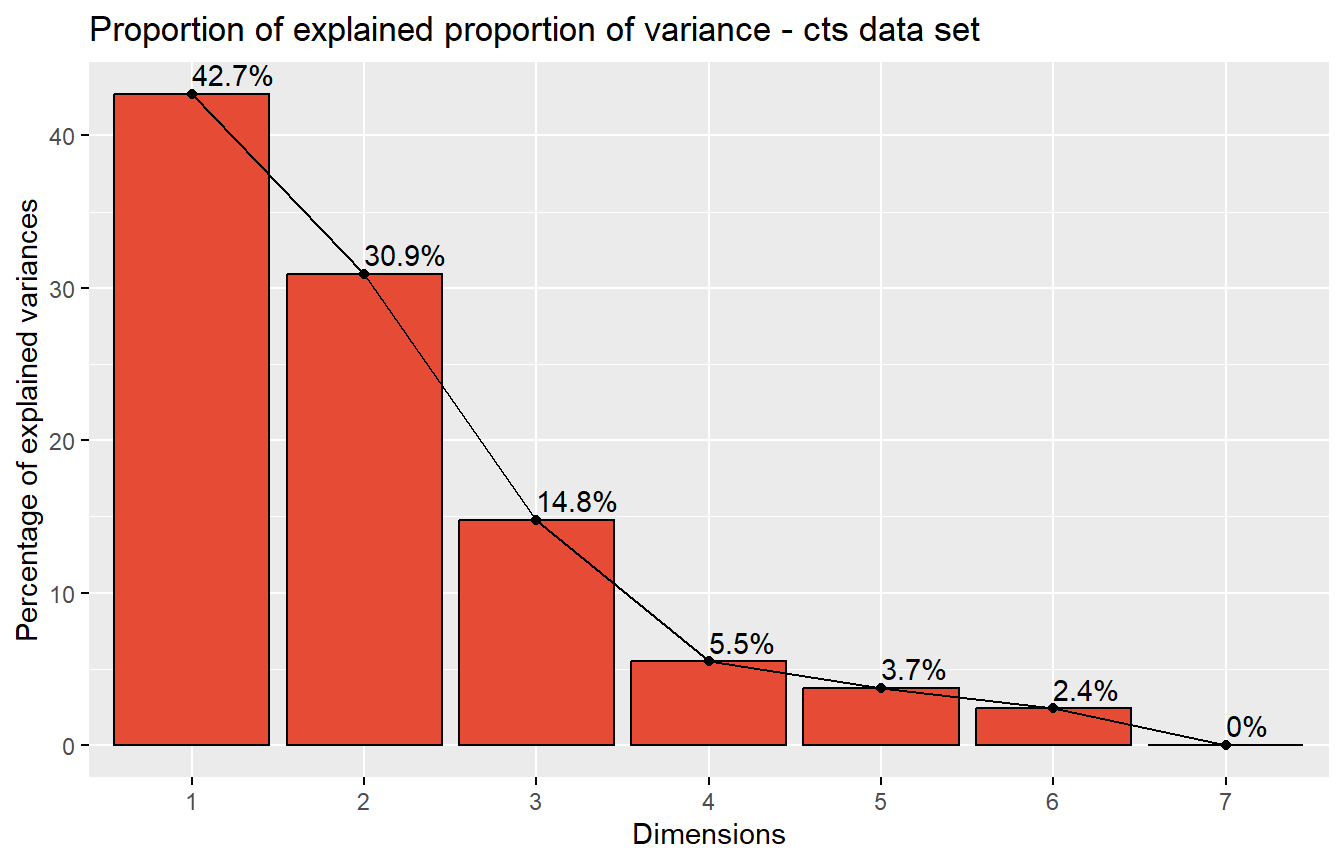

Then, extract genes that are mostly contributed in the principal components. By extracting genes that are primarily responsible for the principal components, it becomes easier to understand the underlying structure of the data and identify potential observations that are associated with certain variables.

# extract the table of the genes with high loadings
top100_pc <- hi_loadings(pcaobj_dds,
                         topN = 100,
                         exprTable = counts(dds))

# Show how experimental data looks like
head(top100_pc) %>% kbl() %>% kable_styling(full_width = FALSE)
treated1 treated2 treated3 untreated1 untreated2 untreated3 untreated4
FBgn0044047 348 118 151 428 667 200 235
FBgn0037683 1496 710 918 1868 2848 1090 1641
FBgn0038381 150 74 79 260 309 121 178
FBgn0040752 5117 2778 2786 5293 10550 4998 4235
FBgn0029801 1628 788 917 1802 3677 1256 1313
FBgn0037635 167 71 92 229 378 139 181

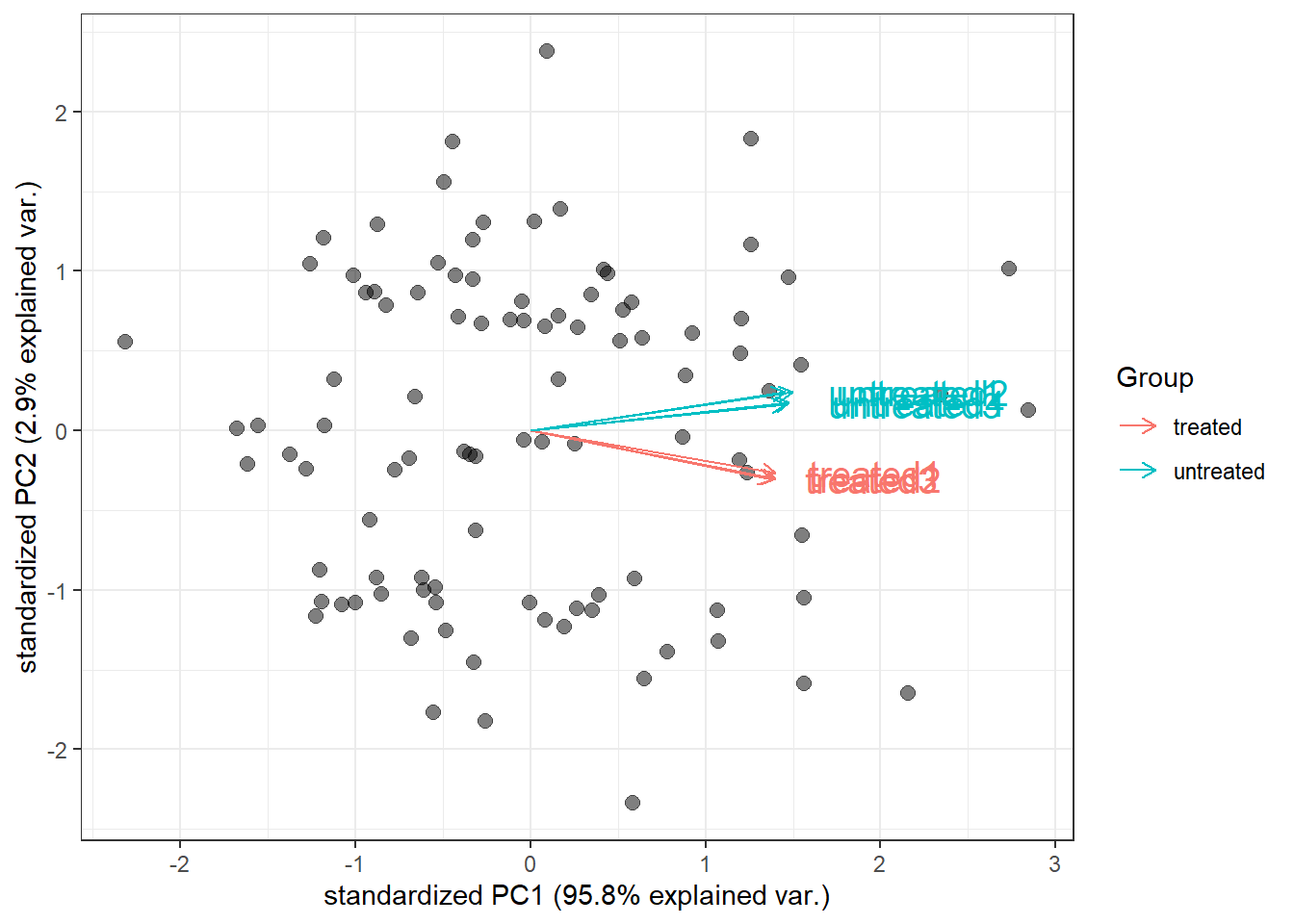
Then, plot PCA biplotgenespca() by compute the principal components of the genes, eventually displaying the samples as in a typical biplot visualization.

groups_cts <- colData(dds)$sample_group

cols_cts <- scales::hue_pal()(2)[groups_cts]

# with many genes, do not plot the labels of the genes
genespca(
  rld_dds,
  ntop = 100,
  choices = c(1, 2),
  arrowColors = cols_cts,
  groupNames = groups_cts,
  useRownamesAsLabels = FALSE,
  varname.size = 5,
  biplot = TRUE,
  alpha = 0.5,
  point_size = 2.5
)

Plots the distribution of expression values, either with density lines, boxplots or violin plots.

distro_expr(rld_dds, plot_type = "violin") + 
  scale_fill_npg() + 
  scale_color_npg()
distro_expr(rld_dds, plot_type = "boxplot") + 
  scale_fill_npg() + 
  scale_color_npg()

See more usage of pcaExplorer: https://federicomarini.github.io/pcaExplorer/articles/pcaExplorer.html#functions-exported-by-the-package-for-standalone-usage

4 Hierarchical Clustering Analysis (Heat maps)

Hierarchical clustering is an unsupervised machine learning algorithm. It is used to group data points into clusters based on their similarity. The algorithm gradually merges or splits clusters after creating a hierarchy. As a result, a dendrogram shows which points are in each cluster and how similar they are.

We’ll demonstrate the hierarchical clustering and plot heat map using pheatmap().

# Create annotation column
annot_column <- data.frame(sample = colnames(top100_pc),
                           group = gsub("[0-9]", "", colnames(top100_pc))) %>% 
  column_to_rownames(var = "sample")

annot_column %>% kbl()
group
treated1 treated
treated2 treated
treated3 treated
untreated1 untreated
untreated2 untreated
untreated3 untreated
untreated4 untreated 
# Create a list of annotation color
sample_pal <- pal_npg()(2)
annot_colors <- list(group = c(treated = sample_pal[1],
                               untreated = sample_pal[2]))
  • Heat map of Top 100 genes that are mostly contributed in the principal components above.
# Heatmap of the top 100 principal components
hm_top100pc <- pheatmap(
  top100_pc,
  scale = "row",
  color = colorRampPalette(rev(brewer.pal(n = 7, name = "RdBu")))(100),
  show_rownames = FALSE,
  name = "Normalized count",
  clustering_distance_rows = "euclidean",
  clustering_distance_cols = "euclidean",
  clustering_method = "complete",
  annotation_col = annot_column,
  annotation_names_col = FALSE,
  annotation_colors = annot_colors,
  cutree_rows = 3,
  annotation_legend = FALSE
)
hm_top100pc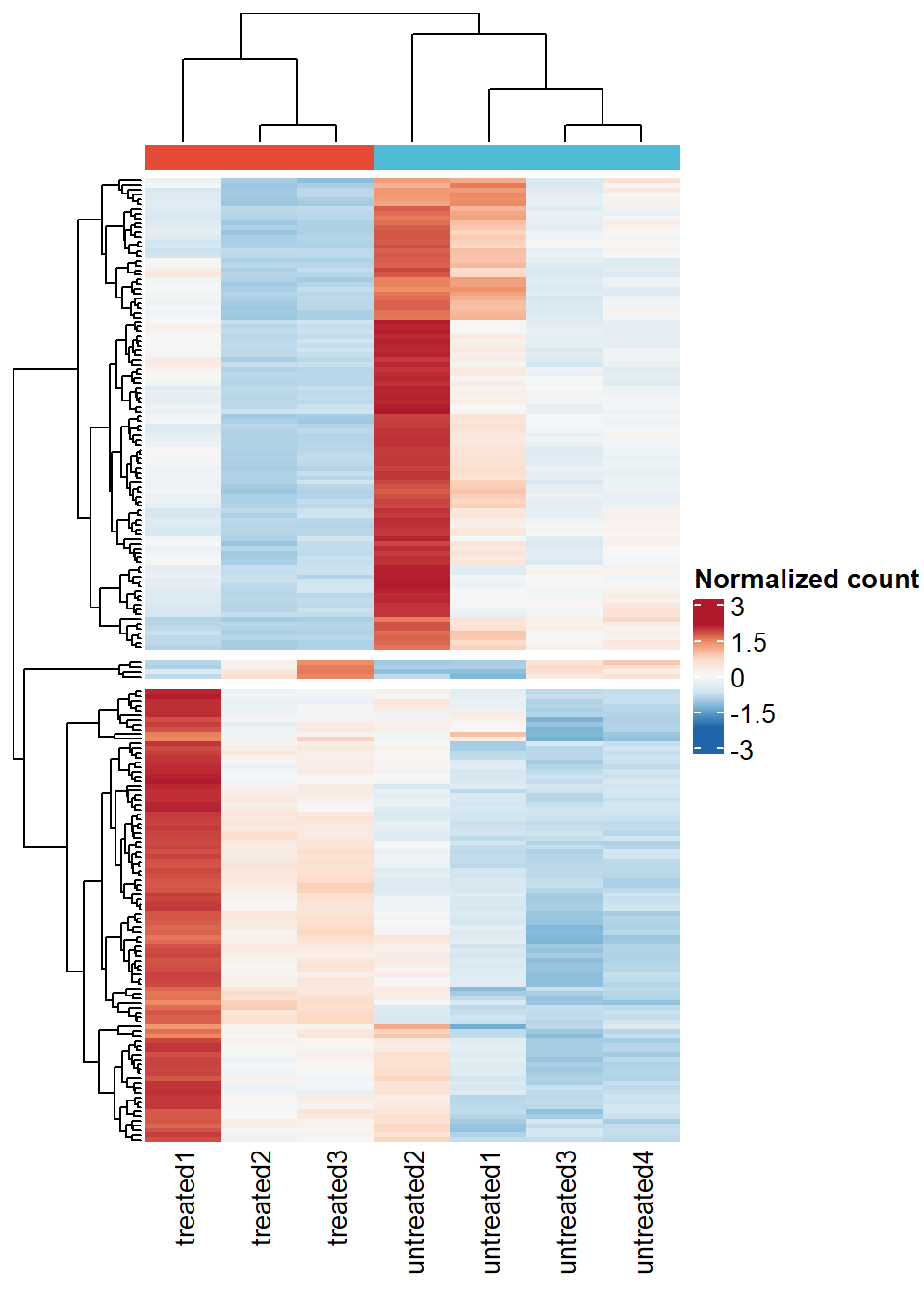

  • Heat map of differentially expressed genes.
# Identify differentially expressed genes
dds_result <- results(object = dds,
                      contrast = c("sample_group", "untreated", "treated"),
                      tidy = TRUE,
                      pAdjustMethod = "fdr")

Filter DEG, we’ll use absolute log2FC > 1 and FDR < 0.05

dds_result_deg <- dds_result %>% 
  filter(padj < 0.05 & abs(log2FoldChange) > 1)

# Extract count matrix of DEGenes
deg_norm_count <- cts_norm[rownames(cts_norm) %in% dds_result_deg$row, ]

# Plot heatmap of DEGs
# Heatmap of the top 100 principal components
hm_deg <- pheatmap(
  deg_norm_count,
  scale = "row",
  color = colorRampPalette(rev(brewer.pal(n = 7, name = "RdBu")))(100),
  show_rownames = FALSE,
  name = "Normalized count",
  clustering_distance_rows = "euclidean",
  clustering_distance_cols = "euclidean",
  clustering_method = "complete",
  annotation_col = annot_column,
  annotation_names_col = FALSE,
  annotation_colors = annot_colors,
  cutree_rows = 2,
  annotation_legend = FALSE)
hm_deg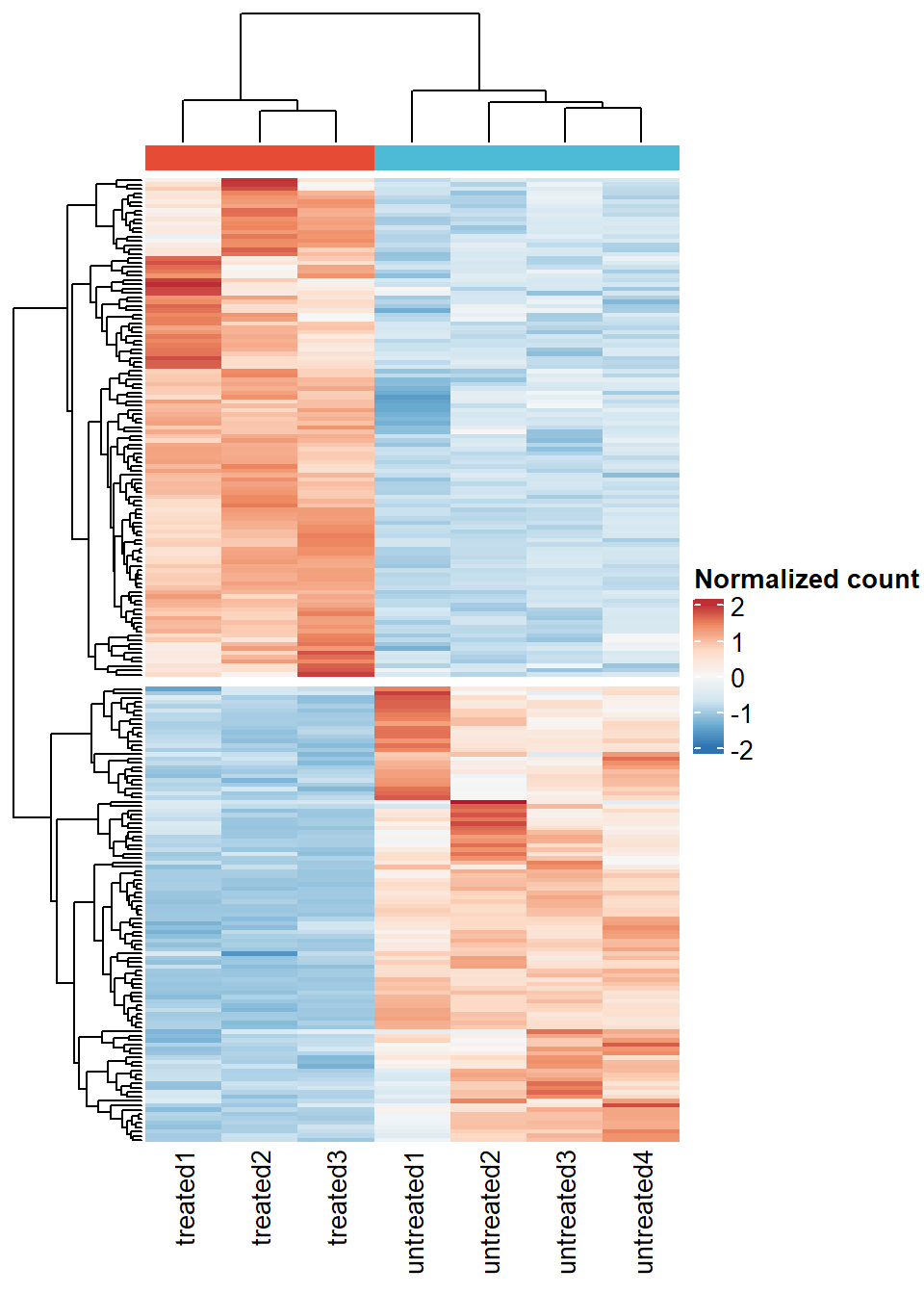

See more pheatmap() usage: https://www.reneshbedre.com/blog/heatmap-with-pheatmap-package-r.html

5 Volcano Plot

volcano_deg <- dds_result %>% 
  mutate(Expression = case_when(
      log2FoldChange >= 1 & padj <= 0.05 ~ "Upregulated",
      log2FoldChange <= -1 & padj <= 0.05 ~ "Downregulated",
      TRUE ~ "Unchanged"))

p_volcano <- EnhancedVolcano(
  volcano_deg,
  lab = volcano_deg$row,
  x = 'log2FoldChange',
  y = 'padj',
  xlim = c(-5,5),
  ylab = bquote( ~ -Log[10] ~ italic(FDR)),
  title = NULL,
  caption = NULL,
  subtitle = NULL,
  pCutoff = 0.05,
  pointSize = 3,
  labSize = 3,
  col = c("grey50", "dodgerblue3", "dodgerblue3", "firebrick2"),
  legendLabels = c("NS", 
                   expression(abs(log[2] ~ FC) > 1),
                   "FDR < 0.05",
                   expression(Pvalue < 0.05 ~ and ~ abs(log[2] ~ FC) > 1))) +
  theme_minimal() +
  theme(legend.position = "bottom",
        panel.border = element_rect(fill = NA, color = "black"),
        panel.grid = element_blank())


p_volcano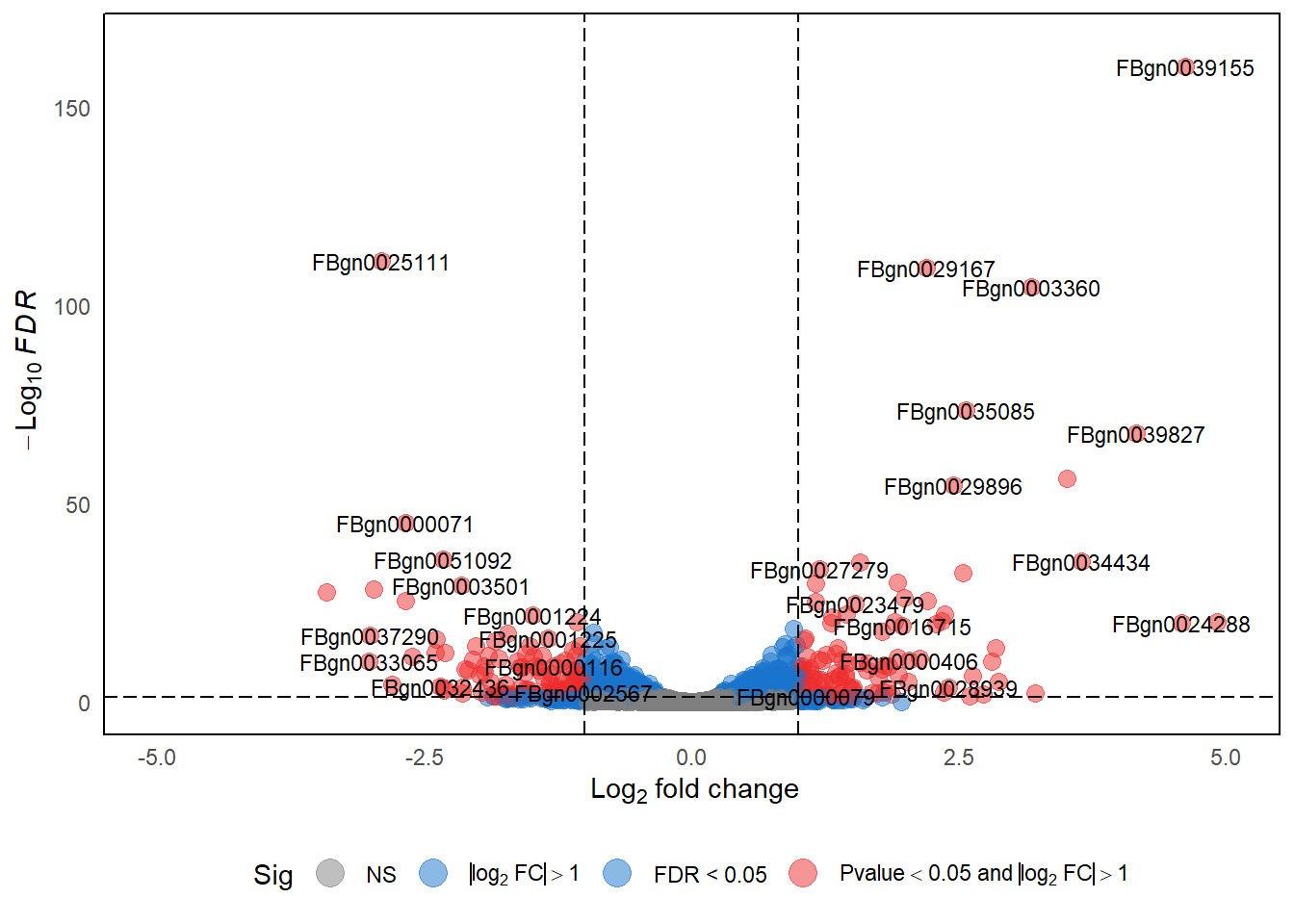

See more EnhancedVolcano() usage: https://bioconductor.org/packages/devel/bioc/vignettes/EnhancedVolcano/inst/doc/EnhancedVolcano.html

6 Venn Diagram and Upset Plot

6.1 Plotting Venn diagram with ggvenn

# Load data
mouse_hallmarks <- read_delim("https://github.com/JirathNuan/r-handviz-workshop/raw/main/datasets/mouse_msigdb_6hallmarks.txt")

# Split into list
lst_mouse_hallmark <- as.list(mouse_hallmarks)
# remove NAs
lst_mouse_hallmark <- lapply(lst_mouse_hallmark, na.omit)

# Chart
ggvenn(
  lst_mouse_hallmark, 
  fill_color = pal_npg()(6),
  stroke_size = 0.5, 
  set_name_size = 3
  )

Venn diagram limitation

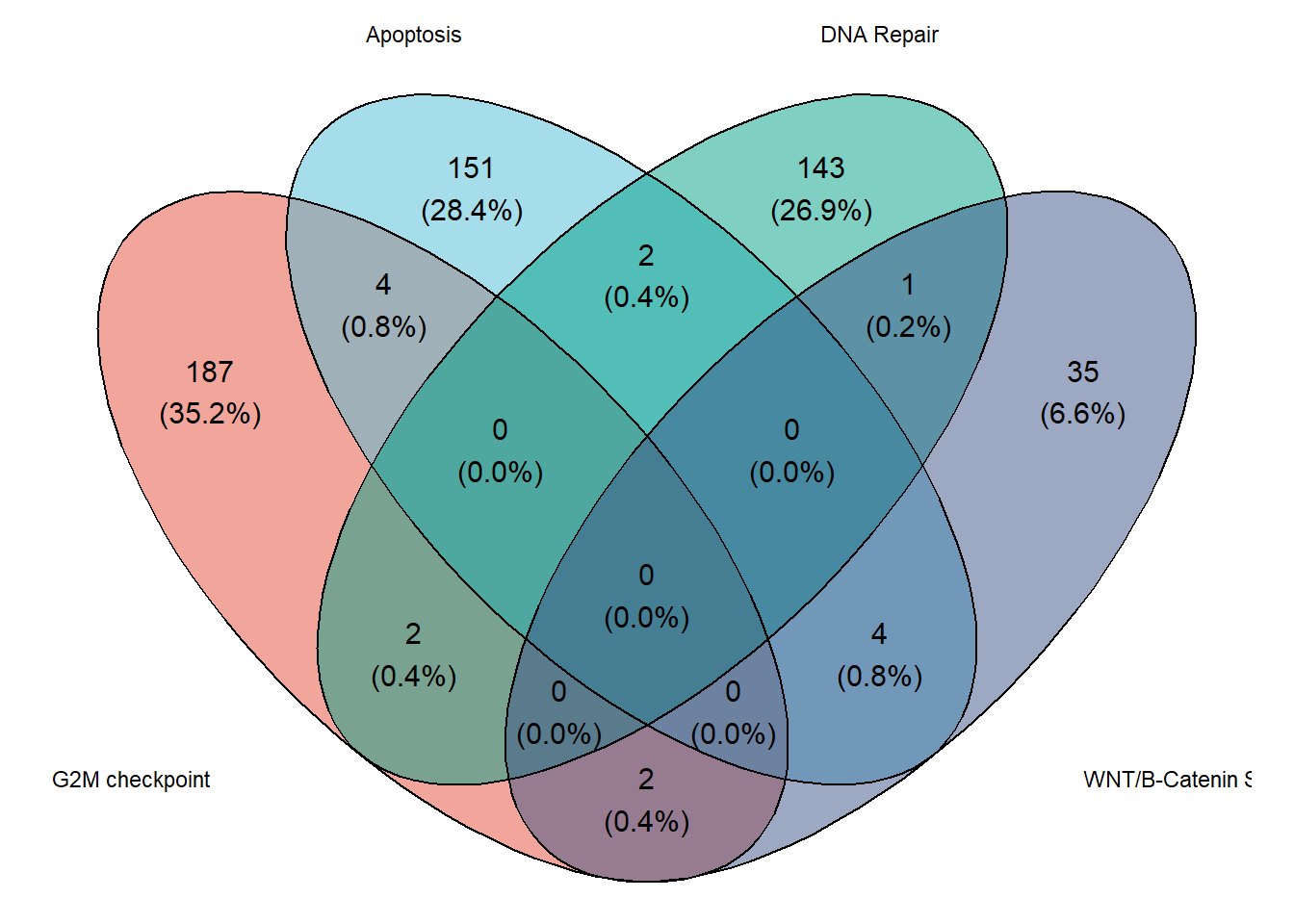
Venn diagrams are simple and easy to interpret, however, ggvenn only allows the visualization of four features at a time. As a result, an alternative of Venn diagram has been developed.

6.2 Venn diagram alternative: Upset Plot

UpSet plots are more efficient than Venn Diagrams at visualizing intersections of multiple sets. They are particularly useful when analyzing large datasets with many variables. They help to identify patterns and relationships between different sets more quickly and easily than other visualizations.

There are 3 different modes of upset plot, distinct (default), intersect, and union. Here we’ll only demonstrate the default mode.

set.seed(123)

# Make present-absent matrix of data list
mouse_hm_mat01 <- list_to_matrix(lst_mouse_hallmark)
# Show how the combination matrix looks like
head(mouse_hm_mat01) %>% kbl()
G2M checkpoint Apoptosis DNA Repair WNT/B-Catenin Signaling Hedgehog Signaling TGF_BETA_SIGNALING
Aaas 0 0 1 0 0 0
Abl1 1 0 0 0 0 0
Ache 0 0 0 0 1 0
Acvr1 0 0 0 0 0 1
Ada 0 0 1 0 0 0
Adam17 0 0 0 1 0 0 
# Make the combination matrix
comb_mat <- make_comb_mat(lst_mouse_hallmark)
comb_mat
A combination matrix with 6 sets and 18 combinations.
  ranges of combination set size: c(1, 183).
  mode for the combination size: distinct.
  sets are on rows.

Top 8 combination sets are:
  G2M checkpoint Apoptosis DNA Repair WNT/B-Catenin Signaling Hedgehog Signaling TGF_BETA_SIGNALING   code size
               x                                                                                    100000  183
                         x                                                                          010000  147
                                    x                                                               001000  143
                                                                                                  x 000001   45
                                                            x                                       000100   31
                                                                               x                    000010   31
               x         x                                                                          110000    4
                         x                                                                        x 010001    4

Sets are:
                      set size
           G2M checkpoint  195
                Apoptosis  161
               DNA Repair  148
  WNT/B-Catenin Signaling   42
       Hedgehog Signaling   36
       TGF_BETA_SIGNALING   53

Referred from a full guide of complexHeatmap: The UpSet plot visualizes the size of each combination set. With the binary code of each combination set, we can calculate the size. There are three modes.

Figure from: https://jokergoo.github.io/ComplexHeatmap-reference/book/upset-plot.html#upset-plot

Plot upset plot

pal_upset <- pal_npg()(4)
# Plot upset following the default upset mode.
upset_mouse_hm <-
  UpSet(
    comb_mat,
    comb_col = pal_upset[1],
    row_names_gp = gpar(fontsize = 10),
    right_annotation = upset_right_annotation(
      comb_mat,
      gp = gpar(fill = pal_upset[2]),
      add_numbers = TRUE
    ),
    top_annotation = upset_top_annotation(
      comb_mat,
      gp = gpar(fill = pal_upset[1]),
      add_numbers = TRUE
    )
  )
upset_mouse_hm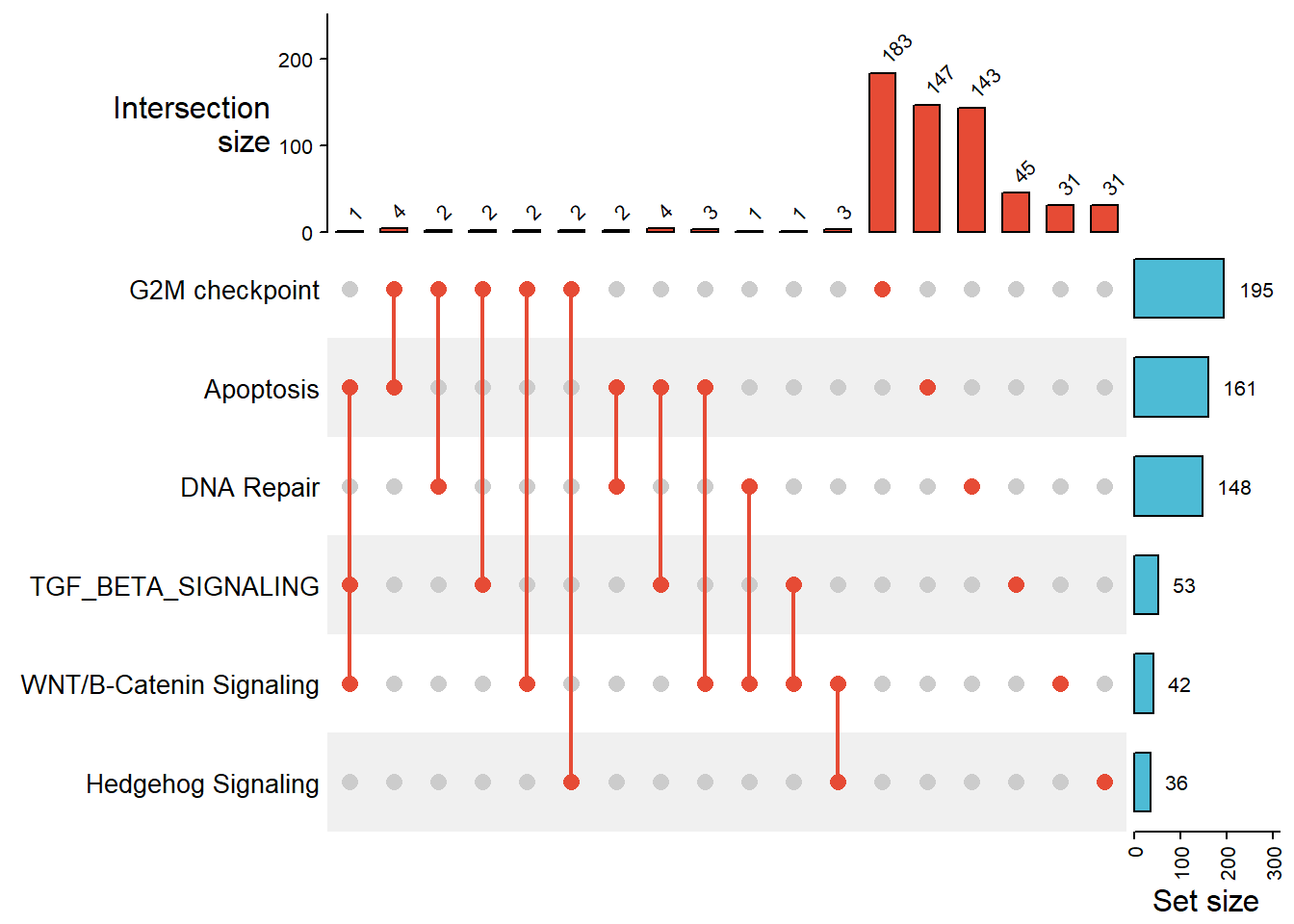

See more UpSet() usage from a complete reference of complexHeatmap: https://jokergoo.github.io/ComplexHeatmap-reference/book/upset-plot.html#upset-plot

7 ggplot2 Based Publication Ready Plots with ggpubr

# Load dataset
mouseLiver_ctg <- read_csv("https://github.com/JirathNuan/r-handviz-workshop/raw/main/datasets/mouseLiver_data_ClinicalTraits.csv")

# Inspect the data
head(mouseLiver_ctg) %>% kbl()
Mice Strain sex weight_g length_cm ab_fat other_fat total_fat 100xfat_weight Trigly Total_Chol HDL_Chol UC FFA Glucose LDL_plus_VLDL MCP_1_phys Insulin_ug_l Glucose_Insulin Leptin_pg_ml Adiponectin Aortic lesions
F2_290 BxH ApoE-/-, F2 Female 36.9 9.9 2.53 2.26 4.79 12.981030 53 1167 50 484 121 437 1117 175.850 924 0.4729437 245462.00 11.274 496250
F2_291 BxH ApoE-/-, F2 Female 48.5 10.7 2.90 2.97 5.87 12.103093 61 1230 32 592 173 572 1198 92.430 5781 0.0989448 84420.88 7.099 NA
F2_292 BxH ApoE-/-, F2 Male 45.7 10.4 1.04 2.31 3.35 7.330416 41 1285 81 460 96 497 1204 196.398 2074 0.2396336 105889.76 5.795 218500
F2_293 BxH ApoE-/-, F2 Male 50.3 10.9 0.91 1.89 2.80 5.566600 271 1299 64 476 122 553 1235 97.466 11874 0.0465723 100398.68 5.495 61250
F2_294 BxH ApoE-/-, F2 Male 44.8 9.8 1.22 2.47 3.69 8.236607 114 1410 50 516 118 535 1360 95.452 9181 0.0582725 130846.30 6.868 243750
F2_295 BxH ApoE-/-, F2 Male 39.2 10.2 3.06 2.49 5.55 14.158163 72 1533 18 620 106 382 1515 144.270 485 0.7876289 75166.22 17.328 104250

7.1 Histogram

gghistogram(
  mouseLiver_ctg,
  x = "weight_g",
  add = "mean",
  rug = TRUE,
  color = "sex",
  fill = "sex",
  bins = 30,
  palette = "npg",
  xlab = "Weight (g)",
  ylab = "Frequency"
)

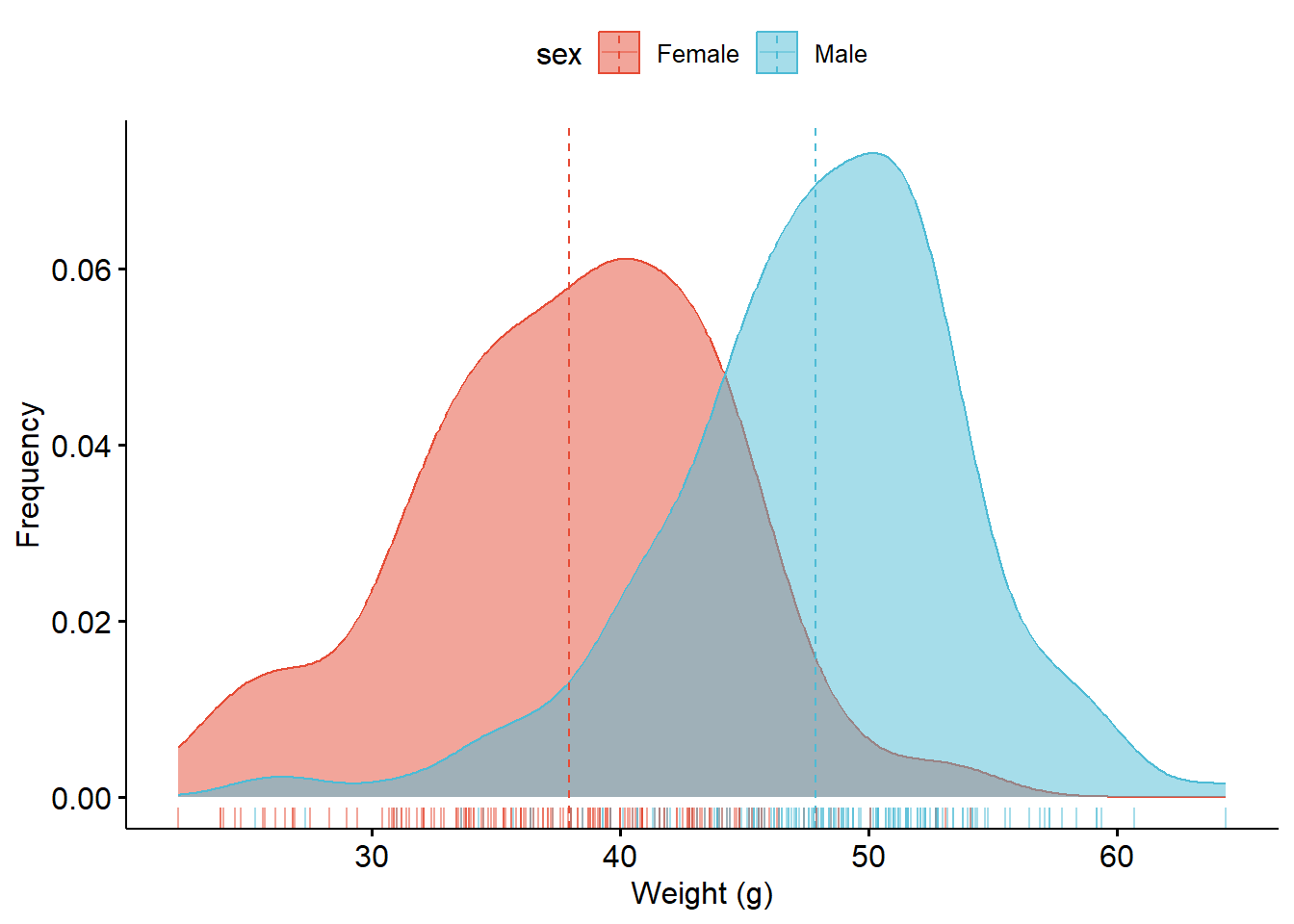
7.2 Density plot

ggdensity(
  mouseLiver_ctg,
  x = "weight_g",
  add = "mean",
  rug = TRUE,
  color = "sex",
  fill = "sex",
  palette = "npg",
  xlab = "Weight (g)",
  ylab = "Frequency"
)

7.3 Simple box plot

p_boxplot <- ggboxplot(ToothGrowth, x = "supp", y = "len",
          color = "supp", palette = "npg",
          add = "jitter",
          xlab = "Supplement type",
          ylab = "Tooth length")
p_boxplot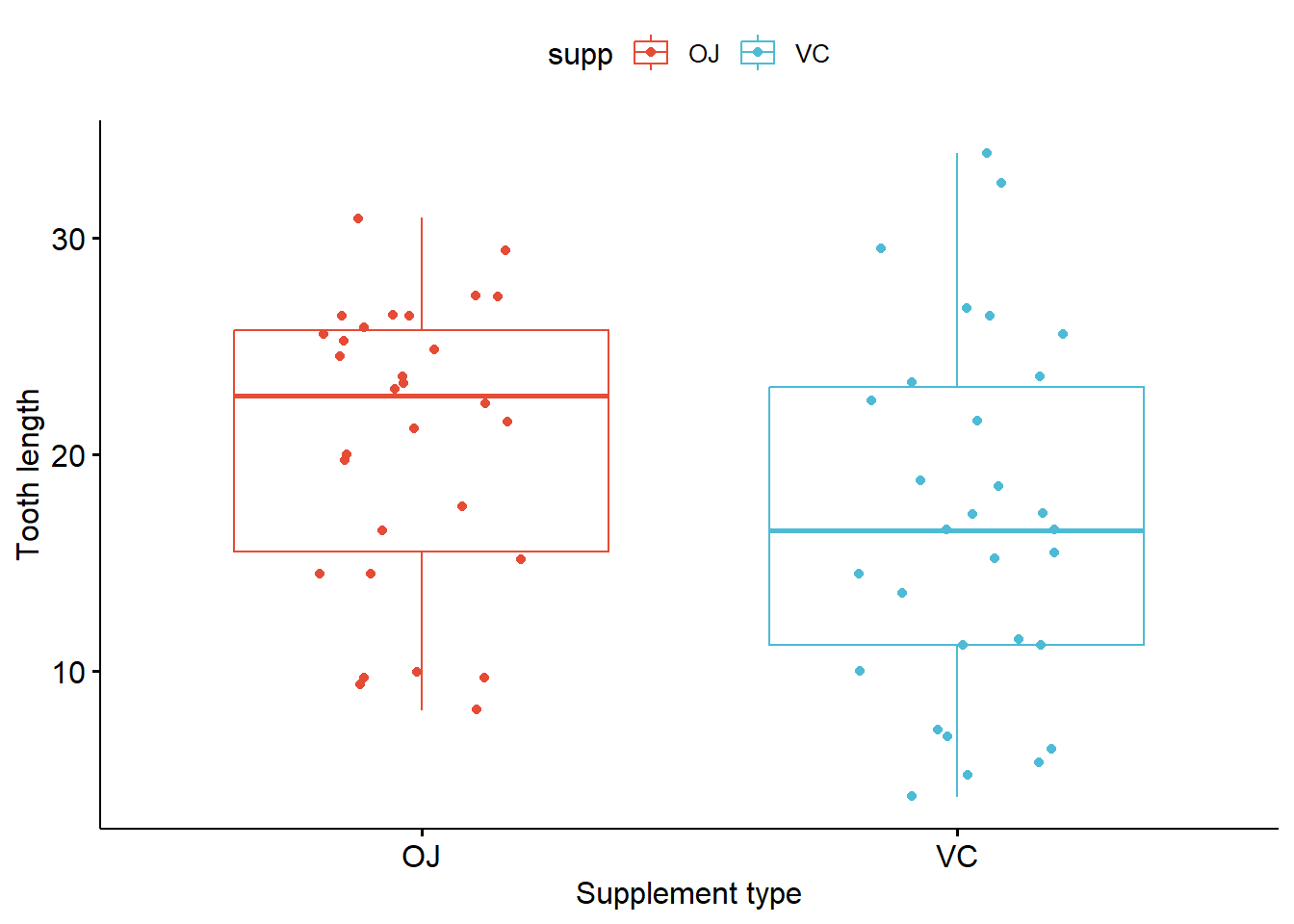

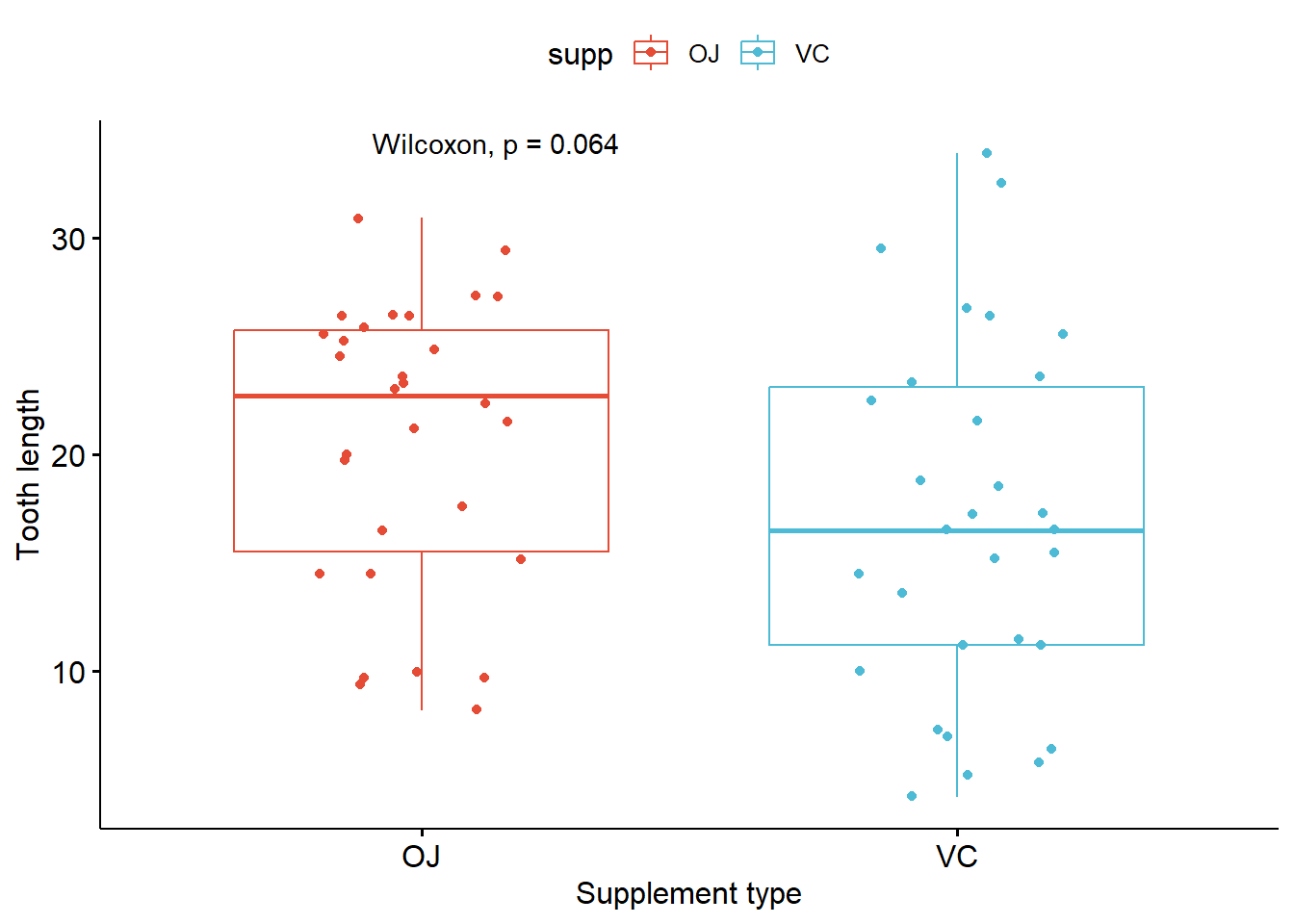
Adding statistical significance to the plot

  • Pairwise comparison
# Try to calculate stat first
compare_means(len ~ supp, data = ToothGrowth, method = "anova")
compare_means(len ~ supp, data = ToothGrowth, method = "wilcox.test")
# Plot box plot with significance
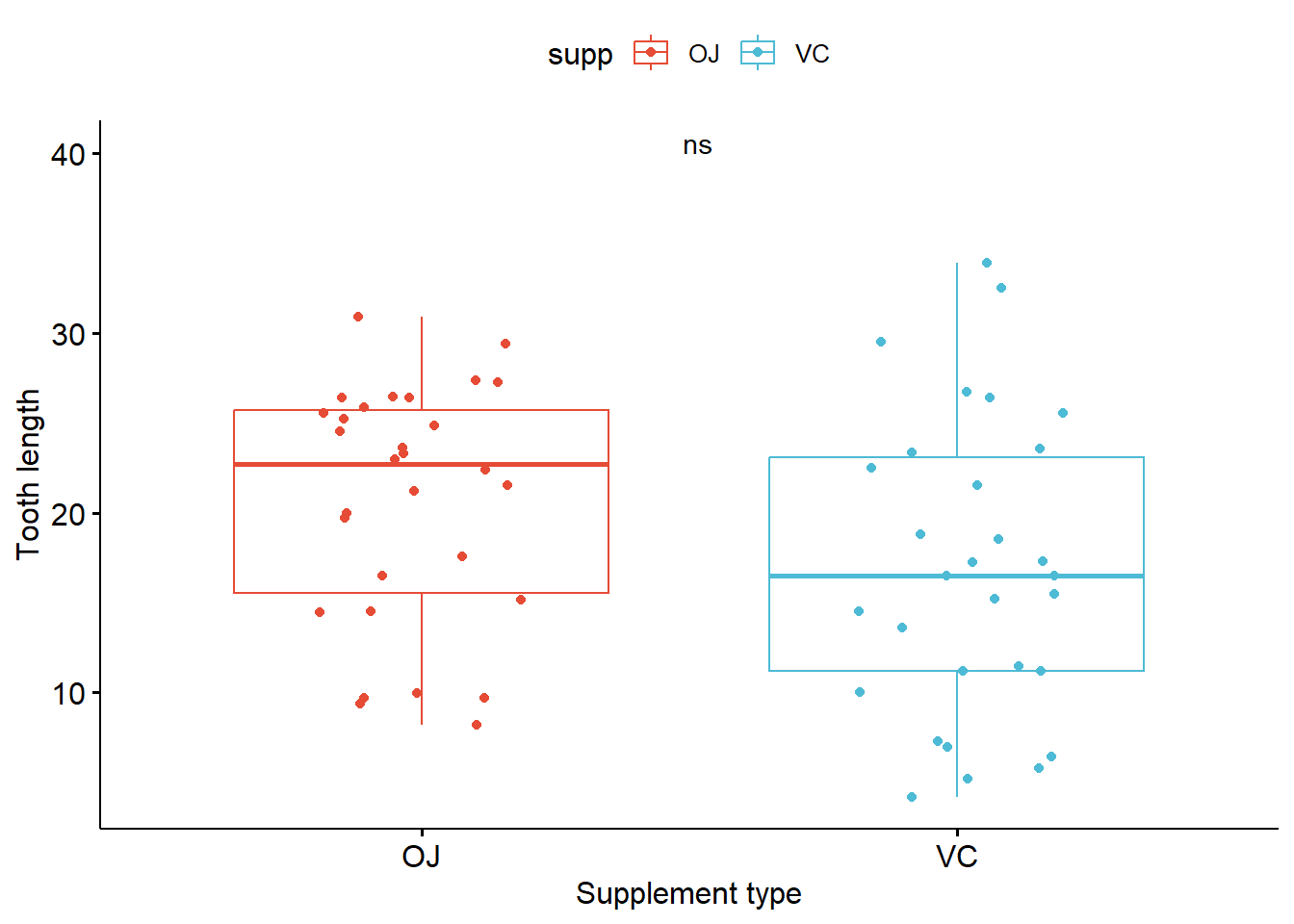
p_boxplot + stat_compare_means(method = "anova")
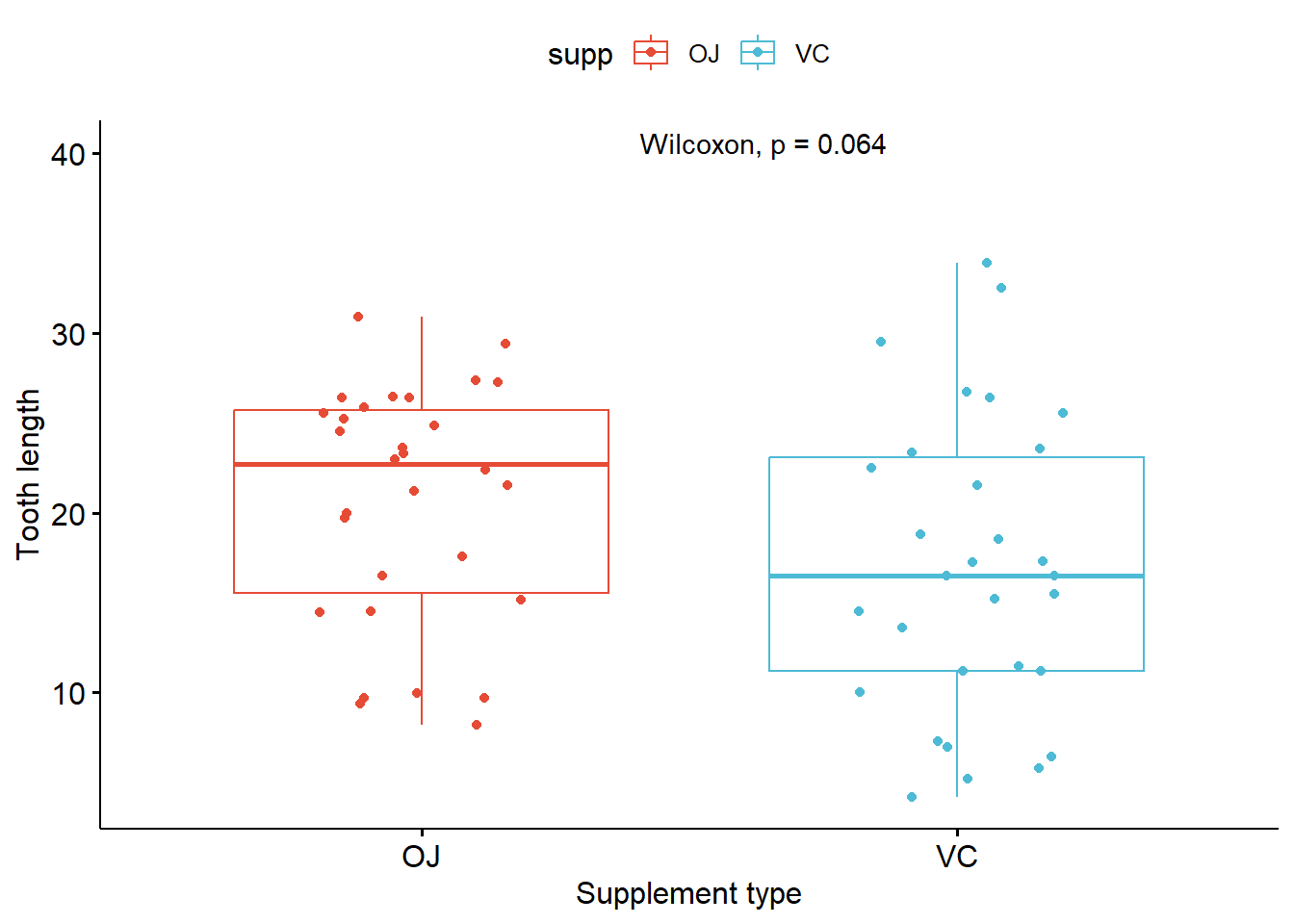
p_boxplot + stat_compare_means(method = "wilcox.test")
# Change style of singnificance notation
p_boxplot + stat_compare_means(method = "anova",
                               aes(label = ..p.signif..),
                               label.x = 1.5,
                               label.y = 40)
p_boxplot + stat_compare_means(method = "wilcox.test",
                               aes(label = "p.signif"),
                               label.x = 1.5,
                               label.y = 40)
# A tibble: 1 × 6
  .y.        p p.adj p.format p.signif method
  <chr>  <dbl> <dbl> <chr>    <chr>    <chr> 
1 len   0.0604  0.06 0.06     ns       Anova 
# A tibble: 1 × 8
  .y.   group1 group2      p p.adj p.format p.signif method  
  <chr> <chr>  <chr>   <dbl> <dbl> <chr>    <chr>    <chr>   
1 len   OJ     VC     0.0645 0.064 0.064    ns       Wilcoxon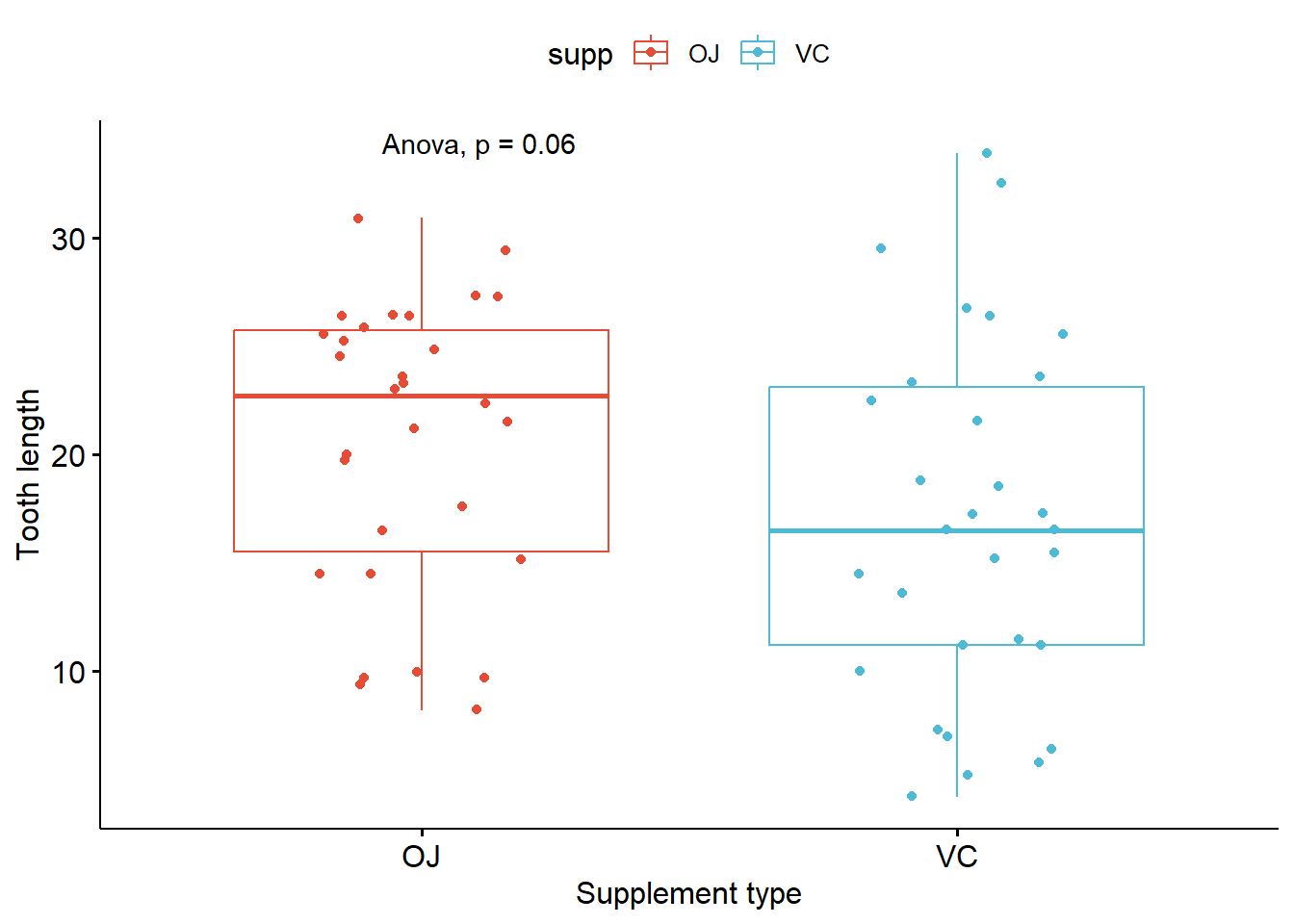

  • Compare more than two groups
# Global test
compare_means(len ~ dose,  data = ToothGrowth, method = "anova")
# Default method = "kruskal.test" for multiple groups
ggboxplot(ToothGrowth, x = "dose", y = "len",
          fill = "dose", palette = "npg")+
  stat_compare_means()
# Change method to anova
ggboxplot(ToothGrowth, x = "dose", y = "len",
          fill = "dose", palette = "npg")+
  stat_compare_means(method = "anova")
# A tibble: 1 × 6
  .y.          p   p.adj p.format p.signif method
  <chr>    <dbl>   <dbl> <chr>    <chr>    <chr> 
1 len   9.53e-16 9.5e-16 9.5e-16  ****     Anova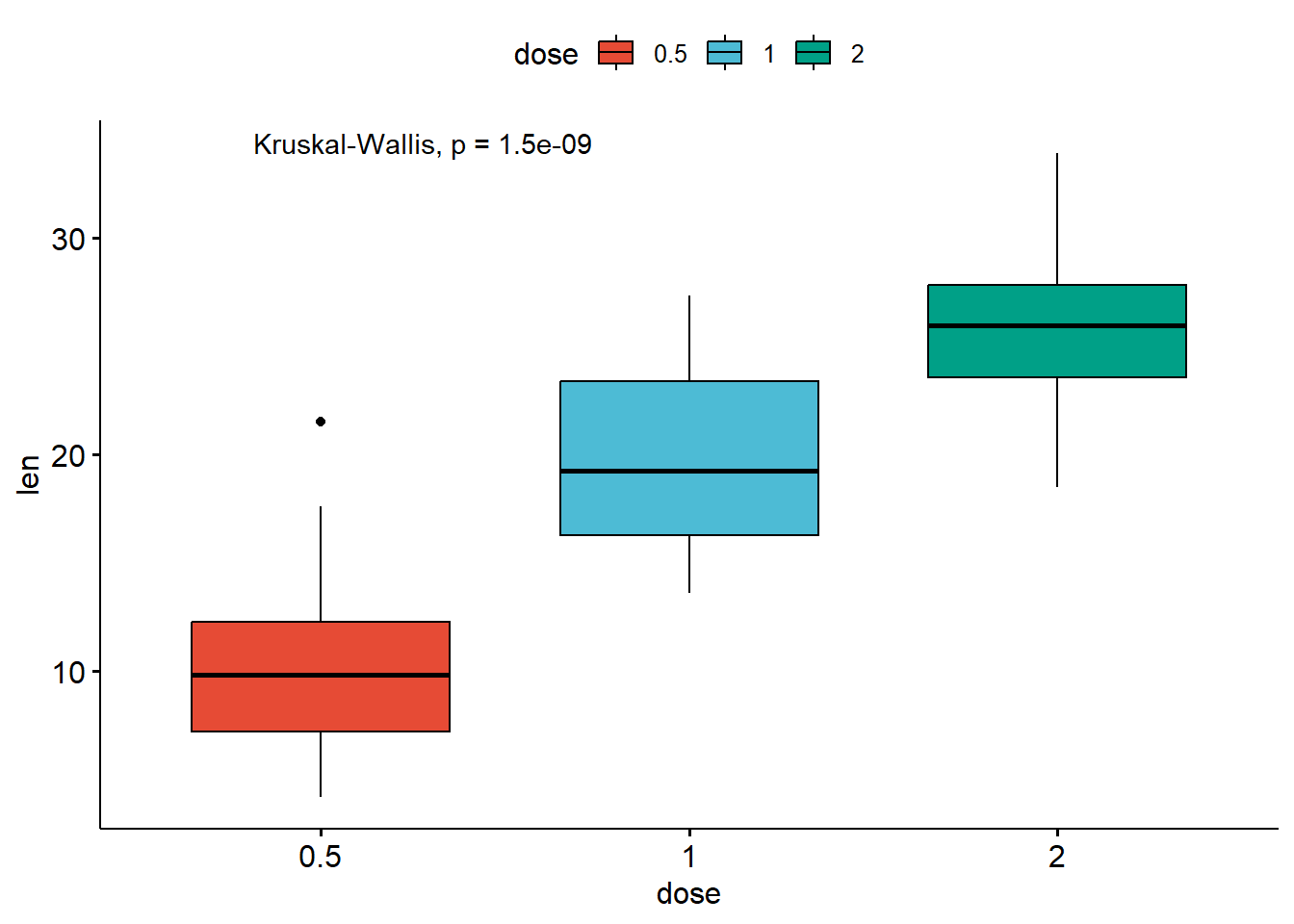 

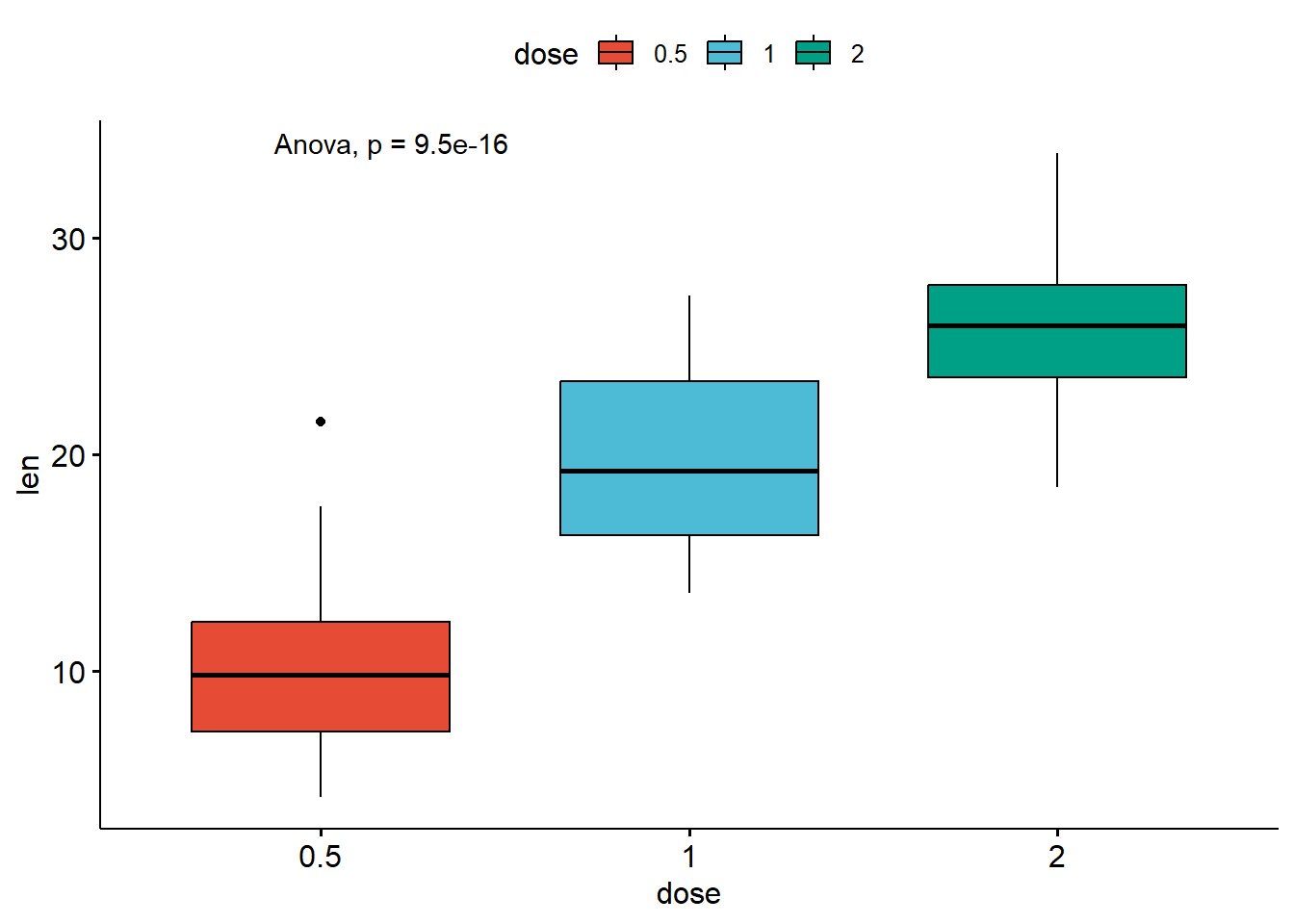
# Perorm pairwise comparisons
compare_means(len ~ dose,  data = ToothGrowth)
# A tibble: 3 × 8
  .y.   group1 group2            p      p.adj p.format p.signif method  
  <chr> <chr>  <chr>         <dbl>      <dbl> <chr>    <chr>    <chr>   
1 len   0.5    1      0.00000702   0.000014   7.0e-06  ****     Wilcoxon
2 len   0.5    2      0.0000000841 0.00000025 8.4e-08  ****     Wilcoxon
3 len   1      2      0.000177     0.00018    0.00018  ***      Wilcoxon
# Visualize: Specify the comparisons you want
my_comparisons <- list(c("0.5", "1"), c("1", "2"), c("0.5", "2"))

ggboxplot(
  ToothGrowth,
  x = "dose",
  y = "len",
  fill = "dose",
  palette = "npg") +
  stat_compare_means(comparisons = my_comparisons) + # Add pairwise comparisons p-value
  stat_compare_means(label.y = 50)     # Add global p-value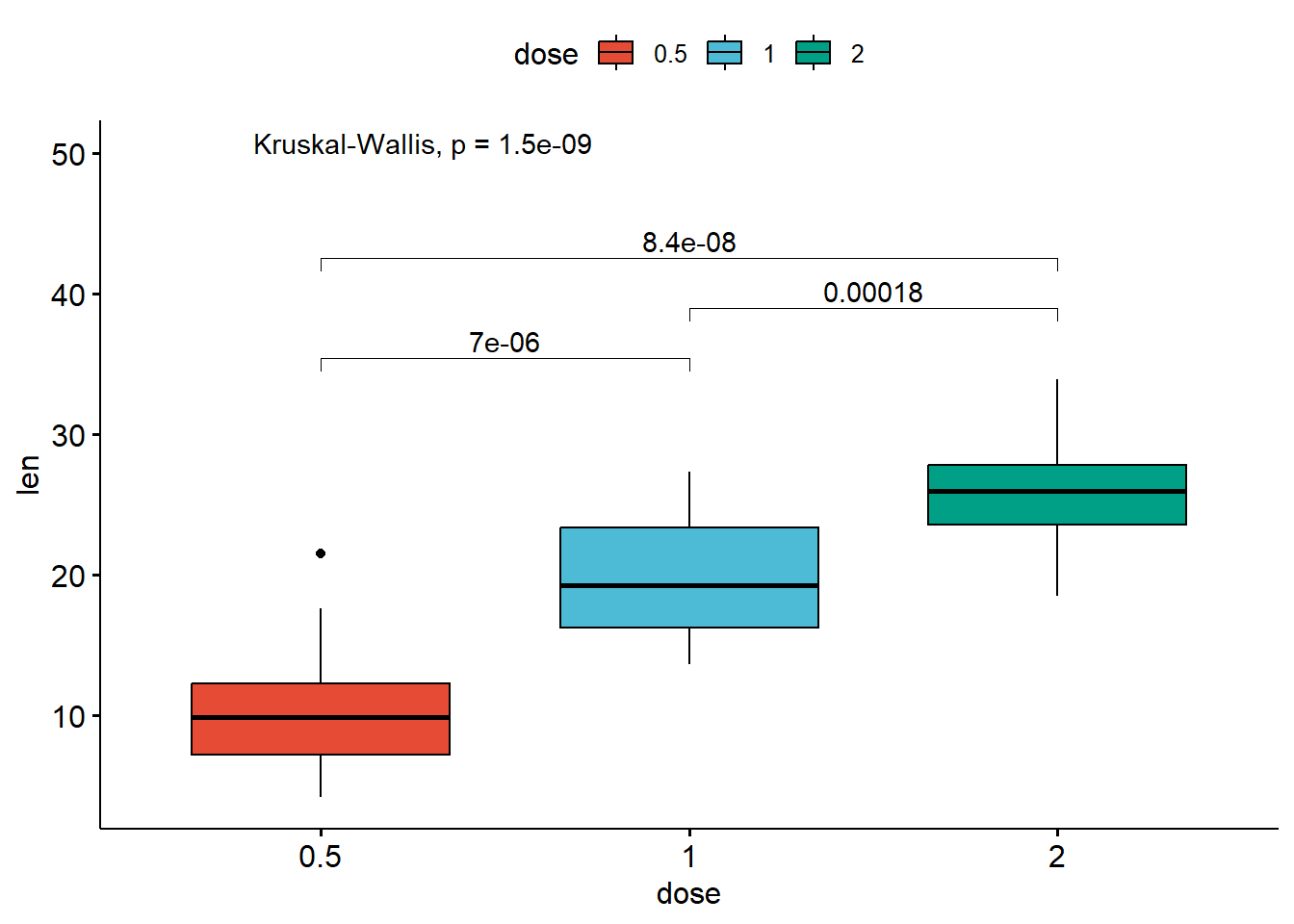

  • Multiple pairwise tests against a reference group
# Pairwise comparison against reference
compare_means(len ~ dose,
              data = ToothGrowth,
              ref.group = "0.5",
              method = "t.test")
# A tibble: 2 × 8
  .y.   group1 group2        p    p.adj p.format p.signif method
  <chr> <chr>  <chr>     <dbl>    <dbl> <chr>    <chr>    <chr> 
1 len   0.5    1      1.27e- 7 1.3 e- 7 1.3e-07  ****     T-test
2 len   0.5    2      4.40e-14 8.80e-14 4.4e-14  ****     T-test
# Visualize
ggboxplot(
  ToothGrowth,
  x = "dose",
  y = "len",
  fill = "dose",
  palette = "npg") +
  stat_compare_means(method = "anova", label.y = 40) +      # Add global p-value
  stat_compare_means(label = "p.signif",
                     method = "t.test",
                     ref.group = "0.5")                    # Pairwise comparison against reference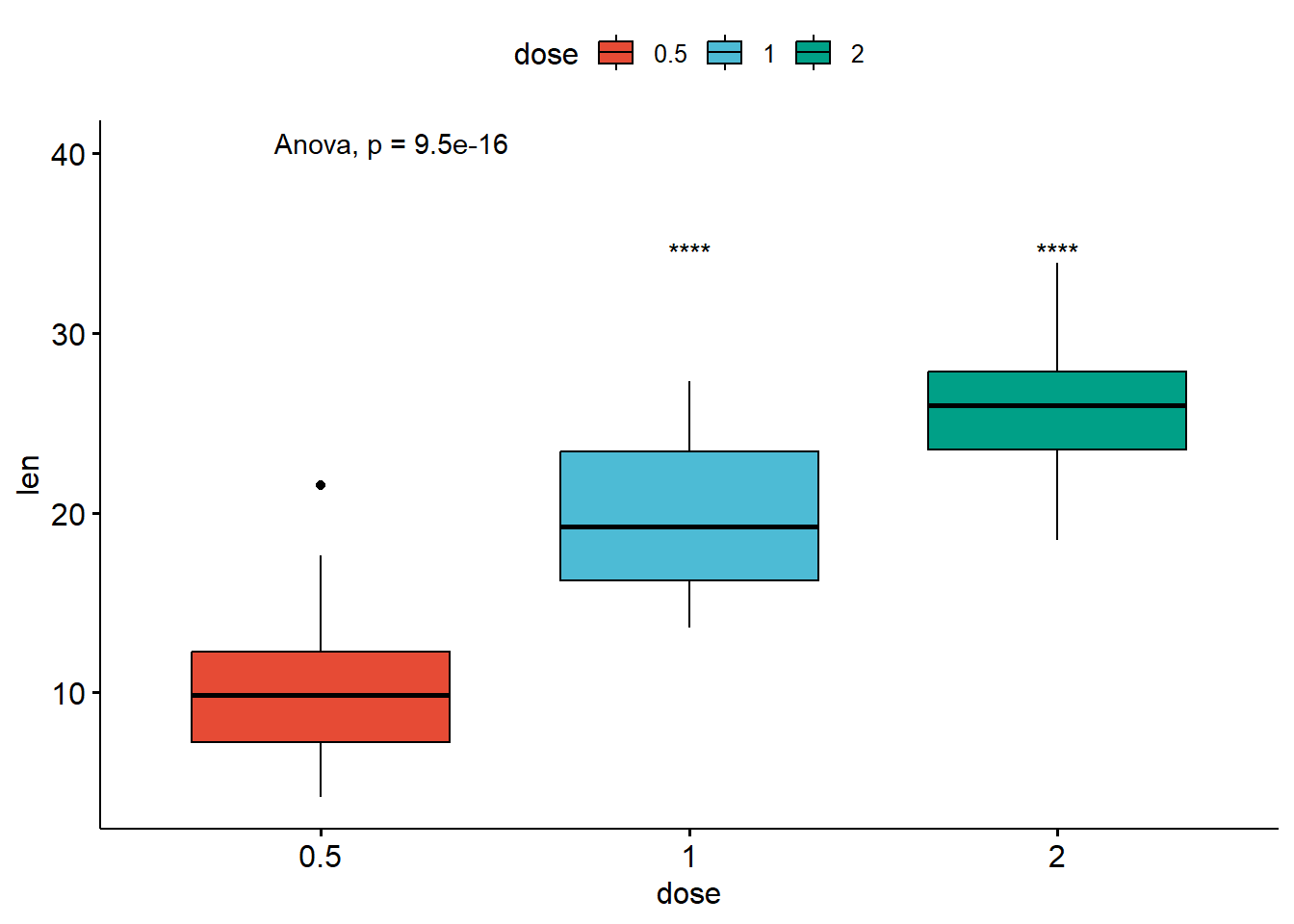

Multiple grouping variables

compare_means(len ~ supp, data = ToothGrowth, group.by = "dose")
# A tibble: 3 × 9
   dose .y.   group1 group2       p p.adj p.format p.signif method  
  <dbl> <chr> <chr>  <chr>    <dbl> <dbl> <chr>    <chr>    <chr>   
1   0.5 len   OJ     VC     0.0232  0.046 0.023    *        Wilcoxon
2   1   len   OJ     VC     0.00403 0.012 0.004    **       Wilcoxon
3   2   len   OJ     VC     1       1     1.000    ns       Wilcoxon
# Box plot facetted by "dose"
p_box <- ggboxplot(
  ToothGrowth,
  x = "supp",
  y = "len",
  color = "supp",
  palette = "jco",
  add = "jitter",
  facet.by = "dose",
  short.panel.labs = FALSE
)
# Use only p.format as label. Remove method name.
p_box + stat_compare_means(label = "p.format")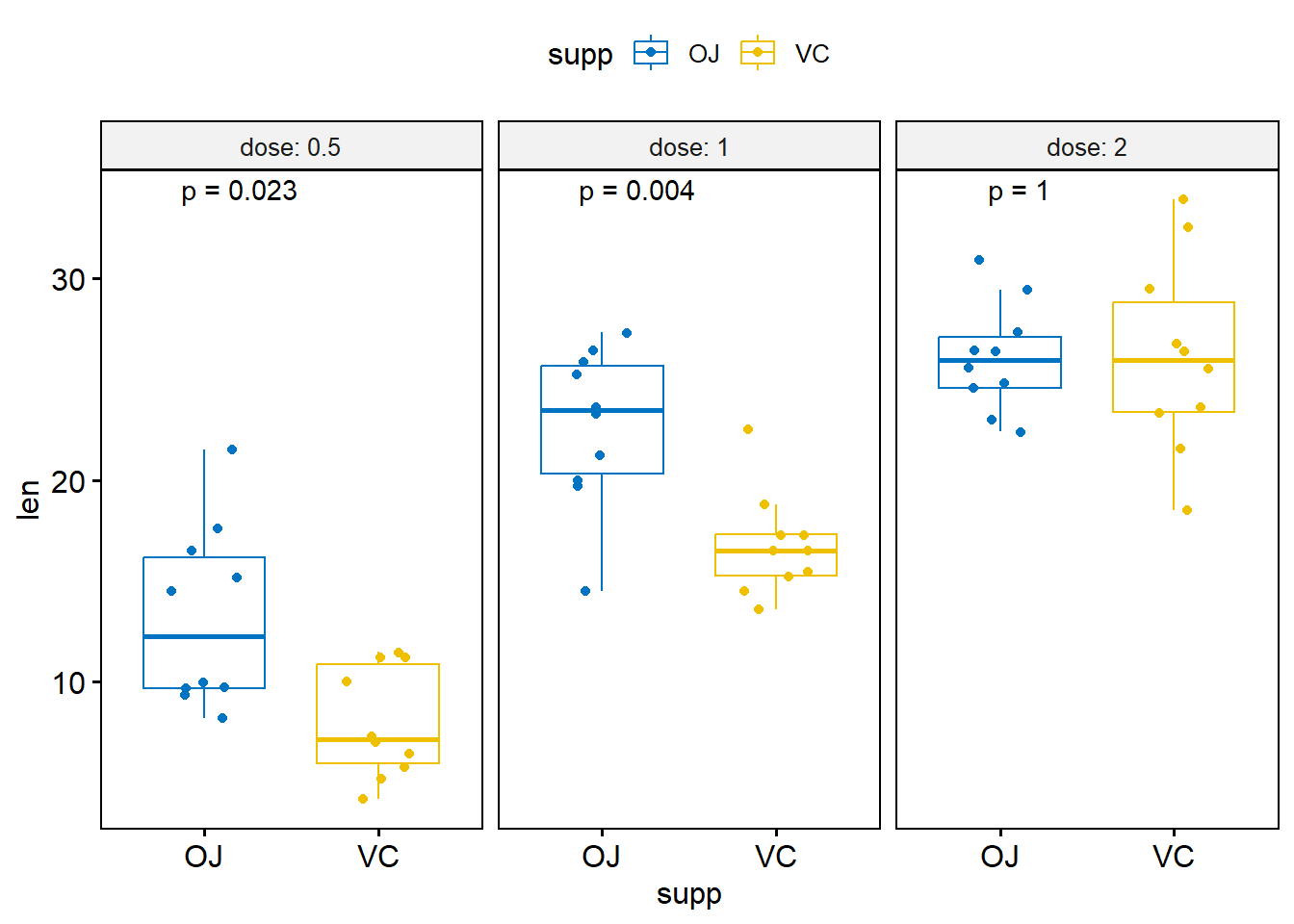

7.4 Bar and line plots (one grouping variable):

ggbarplot(
  ToothGrowth,
  x = "dose",
  y = "len",
  add = "mean_se",
  fill = "supp",
  palette = "npg",
  color = "black",
  position = position_dodge(0.8)) +
  stat_compare_means(aes(group = supp), label = "p.signif", label.y = 29)
ggline(
  ToothGrowth,
  x = "dose",
  y = "len",
  add = "mean_se",
  color = "supp",
  palette = "npg") +
  stat_compare_means(aes(group = supp),
                     label = "p.signif",
                     label.y = c(16, 25, 29))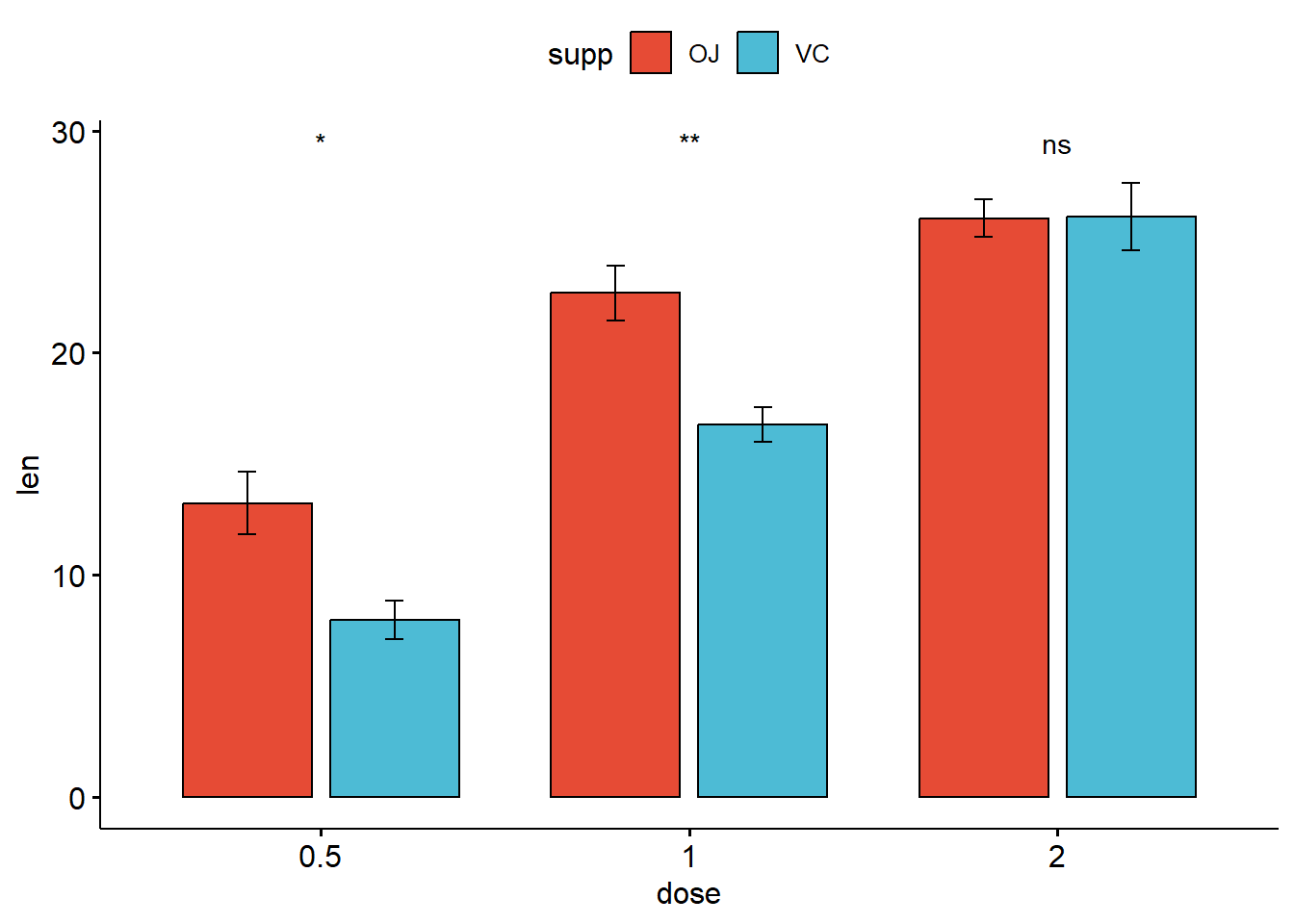

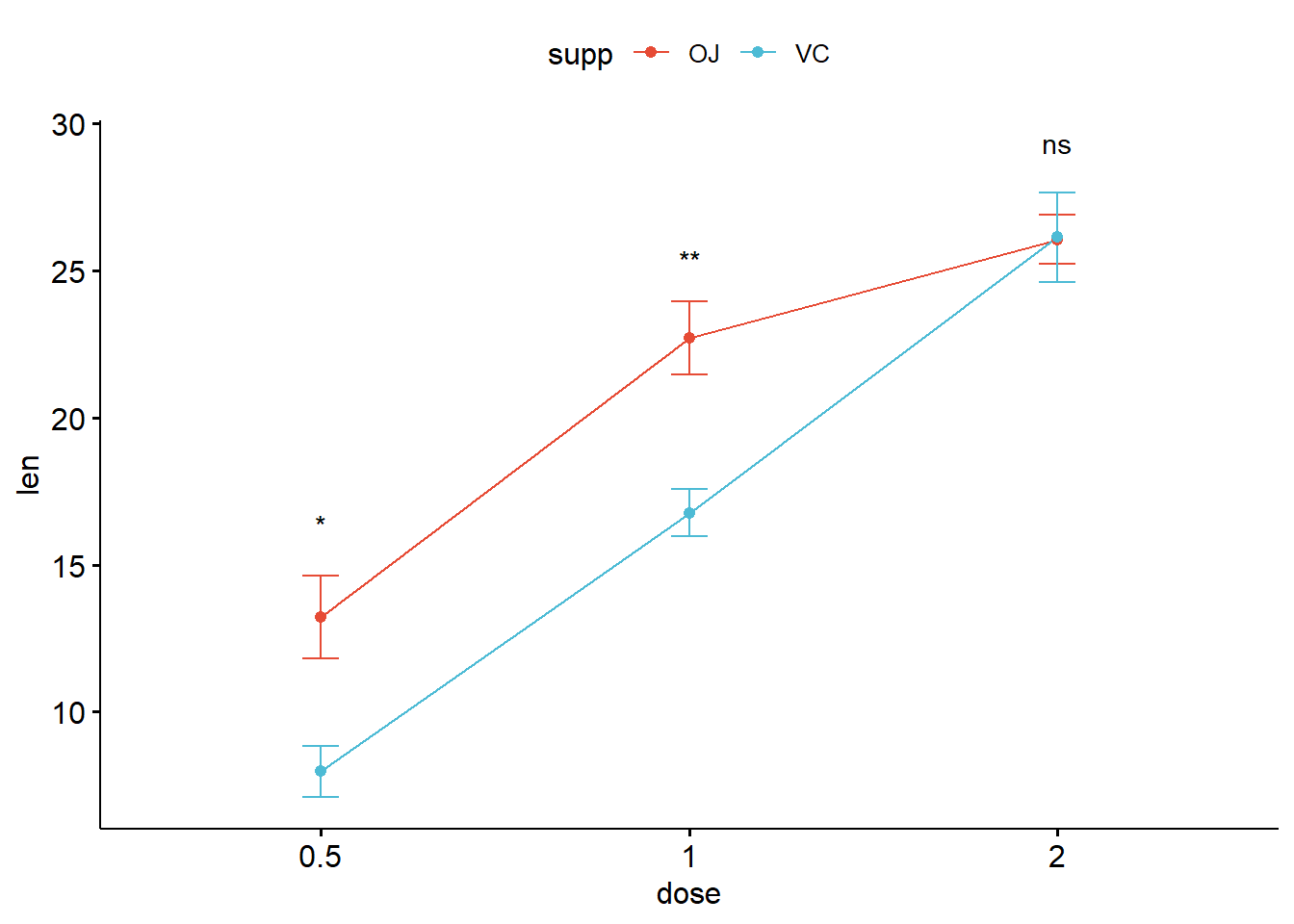
7.5 Scatter plot

p4 <- ggscatter(
  mtcars,
  x = "wt",
  y = "mpg",
  fill = "mpg",
  size = 4,
  shape = 21) +
  gradient_fill(c("blue", "white", "red"))
p4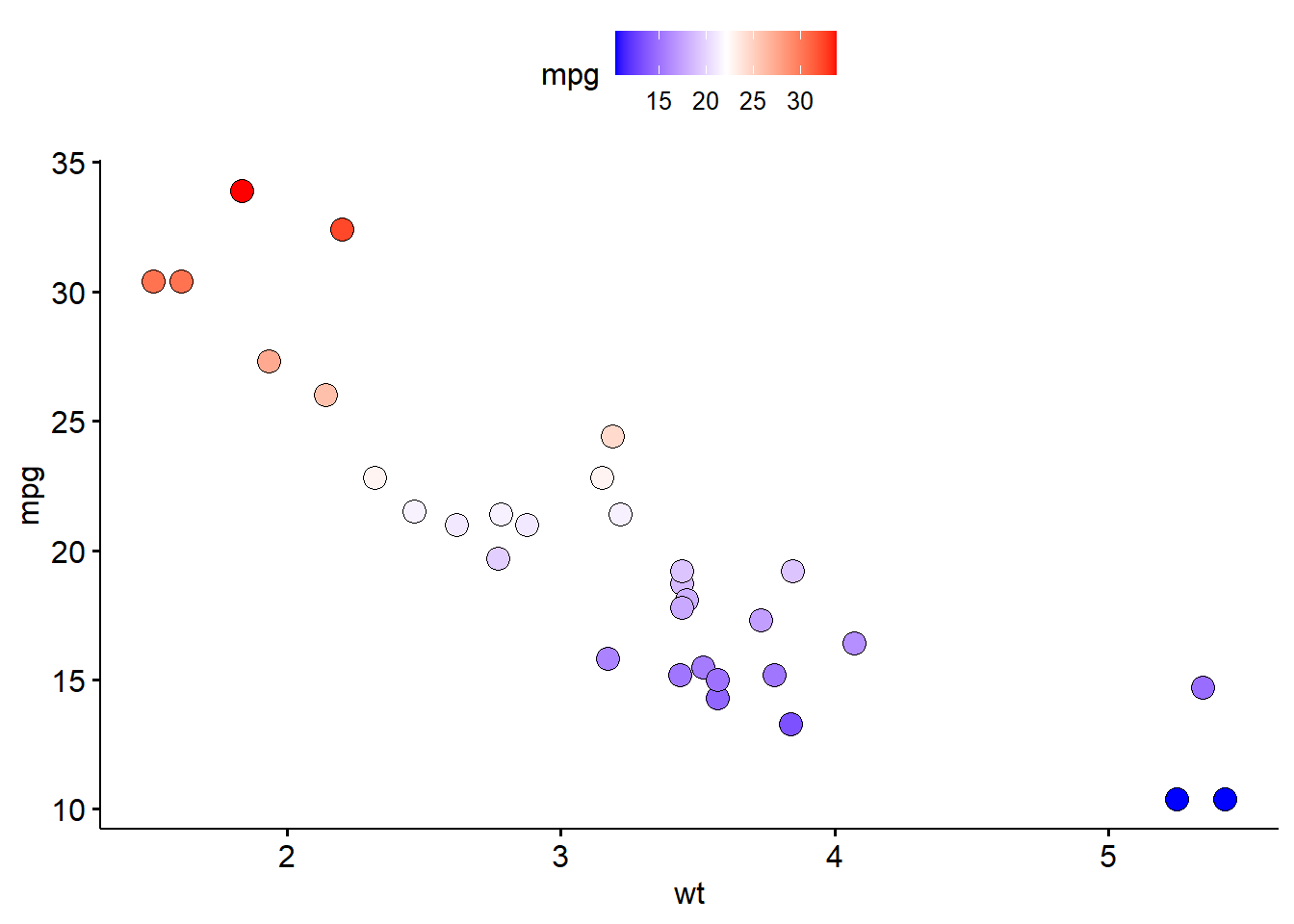

More usage of ggpubr: http://www.sthda.com/english/articles/24-ggpubr-publication-ready-plots/76-add-p-values-and-significance-levels-to-ggplots/.

8 Session info

sessionInfo()
R version 4.3.0 (2023-04-21 ucrt)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 11 x64 (build 22621)

Matrix products: default


locale:
[1] LC_COLLATE=English_United States.utf8 
[2] LC_CTYPE=English_United States.utf8   
[3] LC_MONETARY=English_United States.utf8
[4] LC_NUMERIC=C                          
[5] LC_TIME=English_United States.utf8    

time zone: Asia/Bangkok
tzcode source: internal

attached base packages:
[1] grid      stats4    stats     graphics  grDevices utils     datasets 
[8] methods   base     

other attached packages:
 [1] ggpubr_0.6.0                ggvenn_0.1.10              
 [3] EnhancedVolcano_1.18.0      ggrepel_0.9.3              
 [5] RColorBrewer_1.1-3          ComplexHeatmap_2.16.0      
 [7] ggsci_3.0.0                 factoextra_1.0.7           
 [9] pcaExplorer_2.26.1          DESeq2_1.40.1              
[11] SummarizedExperiment_1.30.1 Biobase_2.60.0             
[13] MatrixGenerics_1.12.0       matrixStats_0.63.0         
[15] GenomicRanges_1.52.0        GenomeInfoDb_1.36.0        
[17] IRanges_2.34.0              S4Vectors_0.38.1           
[19] BiocGenerics_0.46.0         openxlsx_4.2.5.2           
[21] kableExtra_1.3.4            lubridate_1.9.2            
[23] forcats_1.0.0               stringr_1.5.0              
[25] dplyr_1.1.2                 purrr_1.0.1                
[27] readr_2.1.4                 tidyr_1.3.0                
[29] tibble_3.2.1                ggplot2_3.4.2              
[31] tidyverse_2.0.0            

loaded via a namespace (and not attached):
  [1] splines_4.3.0           later_1.3.1             bitops_1.0-7           
  [4] filelock_1.0.2          graph_1.78.0            XML_3.99-0.14          
  [7] lifecycle_1.0.3         rstatix_0.7.2           topGO_2.52.0           
 [10] doParallel_1.0.17       vroom_1.6.3             lattice_0.21-8         
 [13] crosstalk_1.2.0         backports_1.4.1         dendextend_1.17.1      
 [16] magrittr_2.0.3          limma_3.56.1            plotly_4.10.1          
 [19] rmarkdown_2.21          yaml_2.3.7              shinyBS_0.61.1         
 [22] httpuv_1.6.10           NMF_0.26                zip_2.3.0              
 [25] DBI_1.1.3               abind_1.4-5             zlibbioc_1.46.0        
 [28] rvest_1.0.3             RCurl_1.98-1.12         rappdirs_0.3.3         
 [31] circlize_0.4.15         seriation_1.4.2         GenomeInfoDbData_1.2.10
 [34] AnnotationForge_1.42.0  genefilter_1.82.1       pheatmap_1.0.12        
 [37] annotate_1.78.0         svglite_2.1.1           codetools_0.2-19       
 [40] DelayedArray_0.26.2     DT_0.27                 xml2_1.3.4             
 [43] shape_1.4.6             tidyselect_1.2.0        GOstats_2.66.0         
 [46] farver_2.1.1            viridis_0.6.3           TSP_1.2-4              
 [49] BiocFileCache_2.8.0     base64enc_0.1-3         webshot_0.5.4          
 [52] jsonlite_1.8.4          GetoptLong_1.0.5        ellipsis_0.3.2         
 [55] survival_3.5-5          iterators_1.0.14        systemfonts_1.0.4      
 [58] foreach_1.5.2           tools_4.3.0             progress_1.2.2         
 [61] Rcpp_1.0.10             glue_1.6.2              gridExtra_2.3          
 [64] xfun_0.39               ca_0.71.1               shinydashboard_0.7.2   
 [67] withr_2.5.0             BiocManager_1.30.20     Category_2.66.0        
 [70] fastmap_1.1.1           fansi_1.0.4             SparseM_1.81           
 [73] digest_0.6.31           timechange_0.2.0        R6_2.5.1               
 [76] mime_0.12               colorspace_2.1-0        GO.db_3.17.0           
 [79] biomaRt_2.56.0          RSQLite_2.3.1           threejs_0.3.3          
 [82] utf8_1.2.3              generics_0.1.3          data.table_1.14.8      
 [85] prettyunits_1.1.1       httr_1.4.6              htmlwidgets_1.6.2      
 [88] S4Arrays_1.0.1          pkgconfig_2.0.3         gtable_0.3.3           
 [91] blob_1.2.4              registry_0.5-1          XVector_0.40.0         
 [94] htmltools_0.5.5         carData_3.0-5           RBGL_1.76.0            
 [97] clue_0.3-64             GSEABase_1.62.0         scales_1.2.1           
[100] png_0.1-8               knitr_1.42              rstudioapi_0.14        
[103] rjson_0.2.21            tzdb_0.3.0              reshape2_1.4.4         
[106] curl_5.0.0              shinyAce_0.4.2          GlobalOptions_0.1.2    
[109] cachem_1.0.8            parallel_4.3.0          AnnotationDbi_1.62.1   
[112] pillar_1.9.0            vctrs_0.6.2             promises_1.2.0.1       
[115] car_3.1-2               dbplyr_2.3.2            xtable_1.8-4           
[118] cluster_2.1.4           Rgraphviz_2.44.0        evaluate_0.21          
[121] cli_3.6.1               locfit_1.5-9.7          compiler_4.3.0         
[124] rlang_1.1.1             crayon_1.5.2            rngtools_1.5.2         
[127] ggsignif_0.6.4          heatmaply_1.4.2         labeling_0.4.2         
[130] plyr_1.8.8              stringi_1.7.12          viridisLite_0.4.2      
[133] gridBase_0.4-7          BiocParallel_1.34.1     assertthat_0.2.1       
[136] munsell_0.5.0           Biostrings_2.68.0       lazyeval_0.2.2         
[139] pacman_0.5.1            Matrix_1.5-4            hms_1.1.3              
[142] bit64_4.0.5             KEGGREST_1.40.0         shiny_1.7.4            
[145] highr_0.10              broom_1.0.4             igraph_1.4.2           
[148] memoise_2.0.1           bit_4.0.5

References

Brooks, Angela N., Li Yang, Michael O. Duff, Kasper D. Hansen, Jung W. Park, Sandrine Dudoit, Steven E. Brenner, and Brenton R. Graveley. 2010. “Conservation of an RNA Regulatory Map Between Drosophila and Mammals.” Genome Research 21 (2): 193–202. https://doi.org/10.1101/gr.108662.110.